Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Xét \(\Delta BMD\)ta có:
\(MD=MB\left(gt\right)\)=> \(\Delta BMD\)cân tại M
Mà \(B\widehat{M}D=A\widehat{C}B=60^0\)( 2 góc n.t chắn cung AB)
Nên \(\Delta BMD\)đều
b/ Ta có \(\hept{\begin{cases}A\widehat{B}D+D\widehat{B}C=A\widehat{B}C\\D\widehat{B}C+M\widehat{B}C=D\widehat{B}M\\A\widehat{B}C=D\widehat{B}M\left(=60^0\right)\end{cases}}\)
=> \(A\widehat{B}D=M\widehat{B}C\)
Xét \(\Delta ADB\)và \(\Delta MBC\)ta có :
\(\hept{\begin{cases}BD=BM\left(\Delta MBDđều\right)\\BA=BC\left(\Delta ABCđều\right)\\A\widehat{B}D=M\widehat{B}C\left(cmt\right)\end{cases}}\)
=> \(\Delta ADB=\Delta CMB\)(c-g-c)
=>\(AD=MC\)
Ta có: \(\hept{\begin{cases}AM=AD+MD\\MD=MB\left(\Delta MBDđều\right)\\AD=MC\left(cmt\right)\end{cases}}\)
=>\(AM=MB+MC\)
c/
Ta có: \(AB=AC\)<=>\(\widebat{AB}=\widebat{AC}\)
Xét \(\Delta MAB\)và\(\Delta MHC\)ta có:
\(B\widehat{A}M=H\widehat{C}M\)(2 góc n.t chắn cung MB )
\(A\widehat{M}B=H\widehat{M}C\)(2 góc n.t chắn 2 cung = nhau )
=>\(\Delta MAB\)đồng dạng\(\Delta MCH\)
=>\(\frac{MA}{MC}=\frac{MB}{MH}\)=>\(\frac{MA}{MB.MC}=\frac{1}{MH}\)=>\(\frac{MB+MC}{MB.MC}=\frac{1}{MH}\)=>\(\frac{1}{MB}+\frac{1}{MC}=\frac{1}{MH}\left(đpcm\right)\)

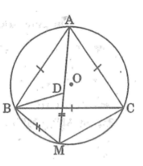
Ta có: ∆ ABD = ∆ CBM (cmt)
suy ra: AD = CM
Ta có: DM = BM ( tam giác MBD đều )
mà AM = AD + DM
suy ra: MA = MC + MB

bạn ơi câu a ko có dữ liệu thì tính sao được còn câu b đợi mk tí mk làm cho
b) vì MD=MB ==> tam giác BDM cân tại M
mà góc BMD=góc ACB=60 độ
do đó tam giác BDM đều ==>DBM=60 độ
ta có ABD+DBC=60 độ
MBC+DBC=60 độ
==> góc ABD= CBM
DO ĐÓ TAM GIÁC ABD= tam giác CBM(c.g.c)
==> AD=CM ==> AD+DM=BM+MC=AM
==> ĐIỀU CẦN CHỨNG MINH

a ) Ta có BM=MD (gt)
=> \(\Delta\)MBD cân tại M
Mặt khác \(\widehat{AMB}=\widehat{ACB}\) ( Hai góc nội tiếp chắn cung AB)
Mà \(\widehat{ACB}=60^0\)( tam giác ABC đều)
Suy ra \(\widehat{AMB}=60^0hay\widehat{DMB}=60^0\)
Vậy \(\Delta MBD\) đều
b) Ta có \(\Delta MBD\) đều ( CMT)
Suy ra : \(\widehat{DMB}=\widehat{DBC}+\widehat{CBM}=60^0\)(1)
Lại có : tam giác ABC đều (gt)
Suy ra : \(\widehat{ABC}=\widehat{ABD}+\widehat{DBC}=60^0\)(2)
Từ (1) và (2) suy ra \(\widehat{ABD}=\widehat{MBC}\)
Xét hai tam giác ABD và CBM ta có
BC=BA (gt)
\(\widehat{ABD}=\widehat{MBC}\left(cmt\right)\)
BD=BM( tam giác MBD đều)
=> \(\Delta ABD=\Delta CBM\left(c.g.c\right)\)
c)\(\Delta ABD=\Delta CBM\left(cmt\right)\)
SUy ra AD=CM
mà AM=AD+DM
SUy ra MA=MC+MD

a)Trên tia MA lấy điểm I sao cho MI=MC
Dễ thấy ΔCIMΔCIM đều ⇒MC=CI⇒MC=CI
Xét 2 tam giác ΔAICΔAICvàΔBMCvàΔBMC có
IC=MCIC=MC
∠IAC=∠MCB∠IAC=∠MCB (vì cùng cộng với ∠BCI=60∘∠BCI=60∘)
AC=BCAC=BC
Do đó ΔAICΔAIC = ΔBMCΔBMC
⇒AI=BM⇒AI=BM
⇒⇒ Đpcm
b) Dễ thấy ΔBAM∼ΔDCMΔBAM∼ΔDCM(g.g)
nên AMCM=BMDM⇒AM.DM=CM.BMAMCM=BMDM⇒AM.DM=CM.BM
⇒AMBM.CM=1MD⇒AMBM.CM=1MD
Áp dụng kết quả câu (a) ta có đpcm
c) Đặt MA=x, MB=y. Ta có
AM2+BM2+CM2=x2+y2+(x−y)2=2(x2+y2−xy)AM2+BM2+CM2=x2+y2+(x−y)2=2(x2+y2−xy) (1)
Kẻ BHBH vuông góc với AMAM
Do ∠BMH=60∘∠BMH=60∘ nên MH=y2,BH2=y2−(y2)2=3y24MH=y2,BH2=y2−(y2)2=3y24
do đó AB2=AH2+BH2=x2+y2−xyAB2=AH2+BH2=x2+y2−xy (2)
Từ (1) và (2) ⇒MA2+MB2+MC2=2AB2⇒MA2+MB2+MC2=2AB2 mà ΔABCΔABC đều
nên AB=R√3
k cho mình nha!!
