Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) CMR: Tứ giác DEIF là hình thoi:
Xét \(\Delta\)ADM: ^ADM=900, I là trung điểm AM => DI=AI=IM (1)
Xét \(\Delta\)AEM: ^AEM=900, I là trung điểm AM => EI=AI=IM (2)
Từ (1) và (2) => DI=EI (*)
Ta có: DI=AI (cmt) => \(\Delta\)AID cân tại I => ^IAD=^IDA hay ^IAD+^IDA=2.^IAD (3)
Tường tự: ^IAE=^IEA => ^IAE+^IEA=2.^IAE (4)
Nhận thấy: ^DIM là góc ngoài \(\Delta\)AID => ^DIM=^IAD+^IDA, thay (3) vào ta đc:
^DIM=2.^IAD (5)
^EIM là góc ngoài \(\Delta\)AIE = >^EIM=^IAE+^IEA, thay (4) vào ta đc:
^EIM=2.^IAE (6)
Từ (5) và (6) => ^DIM+^EIM=2.^IAD+2.^IAE => ^DIE=2.(^IAD+^IAE)=2.^DAE.
Mà ^DAE=^BAC/2=600/2=300 => ^DIE=2.300=600 (**)
Từ (*) và (**) => \(\Delta\)DIE là tam giác đều.
Chứng minh tương tự ta cũng có \(\Delta\)DIF đều => Tứ giác DEIF là hình thoi (đpcm).
b) Đề sai, mình không thấy M,H,K thẳng hàng
Sửa: CMR MH,DI.EF đồng quy.
Gọi S là trung điểm của AH. O là giao điểm của DI và EF (3*)
Xét \(\Delta\)AMH: I là trung điểm AM, S là trung điểm AH
=> IS là đường trung bình \(\Delta\)AMH => IS//MH (7)
Do tứ giác DEIF là hình thoi (cmt) => DI và EF cắt nhau tại trg điểm mỗi đường
=> O là trung điểm của DI và EF.
Xét \(\Delta\)SID: O là trung điểm DI, H là trung điểm SD (H là trực tâm và cũng là trọng tâm \(\Delta\)ABC)
=> OH là đường trung bình \(\Delta\)SID => OH//IS (8)
Từ (7) và (8) => M,O,H thẳng hàng (4*)
Từ (3*) và (4*) => DI,EF,MH đồng quy (đpcm).

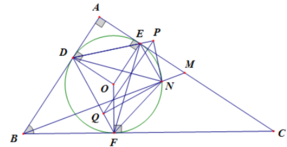
Vì DPN+DQN=90o+90o=180o nên DPNQ là tứ giác nội tiếp
=>QPN=QDN (hai góc nội tiếp cùng chắn cung QN) (5)
Mặt khác DENF là tứ giác nội tiếp nên QDN=FEN (6)
Từ (5) và (6) ta có FEN=QPN (7)
Tương tự ta có: EFN=PQN (8)
Từ (7) và (8) suy ra Δ N P Q ~ Δ N E F ( g . g ) = > P Q E F = N Q N F
Theo quan hệ đường vuông góc – đường xiên, ta có
N Q ≤ N F = > P Q E F = N Q N F ≤ 1 = > P Q ≤ E F
Dấu bằng xảy ra khi Q ≡ F ⇔ NF ⊥ DF ⇔ D, O, N thẳng hàng.
Do đó PQ max khi M là giao điểm của AC và BN, với N là điểm đối xứng với D qua O.

Câu b: Xet tg vuông AEH và tg vuông ABC có
^BAH = ^ACB (cùng phụ với ^ABC)
=> Tg AEH đồng dạng với tg ABC \(\Rightarrow\frac{AE}{AC}=\frac{EH}{AB}\) mà EH=AF (cạnh đối HCN)
\(\Rightarrow\frac{AE}{AC}=\frac{AF}{AB}\Rightarrow AE.AB=AF.AC\)
Câu c:
Ta có AM=BC/2==BM=CM (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
=> tg AMC cân tại M => ^MAC = ^ACB mà ^BAH = ^ACB (cmt) => ^MAC = ^BAH (1)
Ta có ^AHE = ^ABC (cùng phụ với ^BAH) mà ^AHE = ^HAC (góc so le trong) => ^ABC = ^HAC (2)
Gọi giao của AH với EF là O xét tg AOF có
AH=EF (hai đường chéo HCN = nhau)
O là trung điểm của AH vào EF
=> OA=OF => tg AOF cân tại O => ^HAC = ^AFE (3)
Từ (2) và (3) => ^AFE = ^ABC (4)
Mà ^ABC + ^ACB = 90 (5)
Từ (1) (4) (5) => ^MAC + ^AFE = 90
Xét tg AKF có ^AKF = 180 - (^MAC + ^AFE) = 180-90=90 => AM vuông góc EF tại K

a. Em tự giải
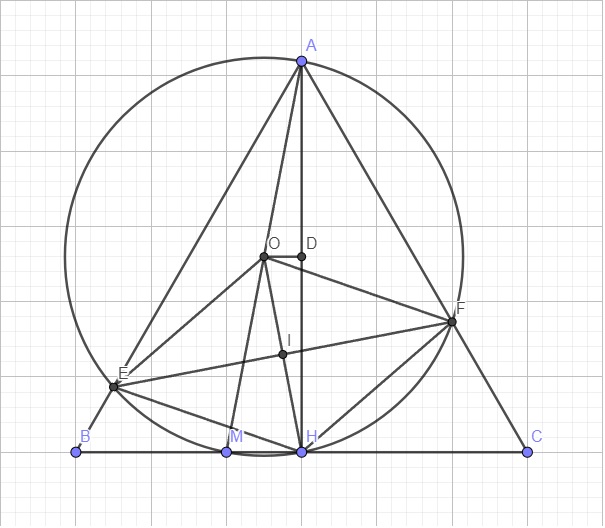
b. Do tam giác ABC đều và AH là đường cao \(\Rightarrow AH\) đồng thời là phân giác góc A
\(\Rightarrow\widehat{BAH}=\widehat{CAH}=\dfrac{1}{2}\widehat{A}=\dfrac{1}{2}.60^0=30^0\)
AEMHF nội tiếp đường tròn tâm O \(\Rightarrow\widehat{HOF}=2.\widehat{CAH}=60^0\) (góc nội tiếp và góc ở tâm cùng chắn cung HF)
Mà \(OH=OF\) (cùng là bán kính) \(\Rightarrow\Delta OHF\) đều (tam giác cân có 1 góc 60 độ)
Tương tự ta có \(\widehat{HOE}=60^0\Rightarrow\Delta OHE\) đều
\(\Rightarrow OE=OF=HE=HF\Rightarrow OEHF\) là hình thoi
c.
Gọi D là trung điểm AH \(\Rightarrow OD\perp AH\) \(\Rightarrow OH\ge DH\Rightarrow OH\ge\dfrac{1}{2}AH\Rightarrow OH\ge\dfrac{a\sqrt{3}}{2}\)
Gọi I là giao điểm EF và OH \(\Rightarrow I\) là tâm hình thoi OEHF
\(S_{OEHF}=2S_{OHE}=2EI.OH=2\sqrt{OE^2-OI^2}.OH\)
\(=2OH.\sqrt{OH^2-\left(\dfrac{OH}{2}\right)^2}=OH^2\sqrt{3}\ge\left(\dfrac{a\sqrt{3}}{2}\right)^2.\sqrt{3}=\dfrac{3a^2\sqrt{3}}{2}\)
Dấu "=" xảy ra khi \(OH=DH\Leftrightarrow O\) trùng D
\(\Rightarrow M\) trùng H