Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

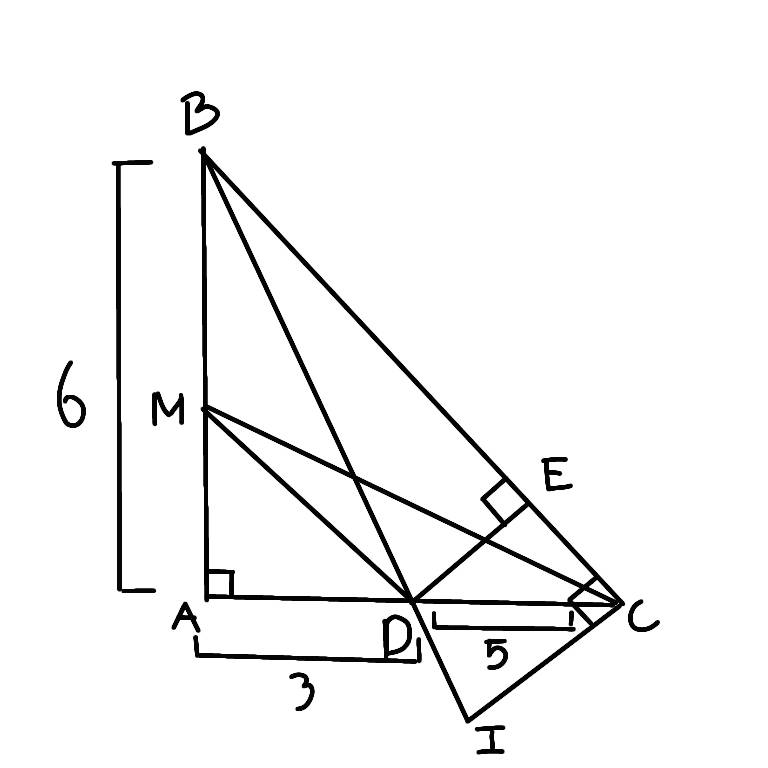 a. Tính BC
a. Tính BC
BC^2 = AC^2 + AB^2
BC^2 = 6^2 + ( AD + DC )^2 = 8^2
BC^2 = 36 + 64 = 100
BC = căng bậc 100 = 10 cm
Tính tỉ số diện tích
Xét tam giác ABC có MD // BC
tam giác AMD ~ tam giác ABC
=>Diện tích tam giác AMD / Diện tích tam giác ABC = (AD/AC)^2=(3/8)^2=9/16 cm2
b.Xét tam giác AMD và tam giác EDC có
Góc MAD = góc CED = 90° (gt)
Góc D chung
=> tam giác AMD ~ tam giác EDC (g.g)
=>MD/AD = DC/EC
=>MD.EC=AD.DC
c. Xét tam giác BCI và tam giác BDE có
Góc BCI = Góc BED = 90°(gt)
Góc B chung
=> Tam giác BCI ~ tam giác BDE(g.g)
=> BC/BI = BD/BE
=> BC.BE = BI.BD(1)
Xét tam giác CBA và tam giác CDE có
Góc CAB = góc CED =90° (gt)
Góc C chung
=> Tam giác CBA ~ tam giác CDE(g.g)
=> CB/CA=CD/CE
=> CB.CE = CA.CD(2)
Từ (1) và (2) ta cộng cho 2 vế
=>BC.BE + CB.CE = BD.BI + CA.CD
=>(BE+CE)BC = BD.BI + CA.CD
=> BC.BC = BD.BI + CA.CD
=> BC^2 = BD.BI + CA.CD

a) Ta có EM là đường trung bình của tam giác BCD Þ ĐPCM.
b) DC đi qua trung điểm D của AE và song song với EM Þ DC đi qua trung điểm I của AM.
c) Vì DI là đường trung bình của tam giác AEM nên DI = (1/2) EM.(1)
Tương tự, ta được: EM = (1/2)DC (2)
Từ (1) và (2) Þ DC = 4DI
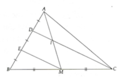

a:Xét ΔBDC có
M là trung điểm của BC
ME//DC
DO đó: E là trung điểm của DB
=>DE=EB(1)
Xét ΔAEM có
I là trung điểm của AM
ID//EM
Do đó: D là trung điểm của AE
=>AD=DE(2)
Từ (1) và (2) suy ra AD=DE=EB
b: Xét ΔBDC có
M là trung điểm của BC
E là trung điểm của BD
Do đó: ME là đường trung bình
=>ME=CD/2
Xét ΔAEM có
I là trung điểm của AM
D là trung điểm của AE
Do đó: ID là đường trung bình
SUy ra: \(ID=\dfrac{ME}{2}=\dfrac{CD}{2}:2=\dfrac{CD}{4}\)