Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cậu tự vẽ hình
a. Xét tg ABC có:
BC2= 102=100
AB2 + AC2= 62 + 82 = 36 + 64 = 100
=> BC2=AB2 + AC2
=> Tam giác ABC vuông tại A (định lý Py-ta-go đảo)
b. Xét △BKM và △CKD vuông tại K có:
MK chung
BK=KC (K là trung điểm BC)
=> △BKM = △CKD (2cgv)
=> BM=CM (2 cạnh tương ứng)
Xét △DMC vuông tại D và △AMB vuông tại A có:
MB=CM (cmt)
góc BMC chung
=> △DMC = △AMB (ch-gn)
=> AB=DC (2 cạnh tương ứng)

a: Xét ΔABC có AB<AC
mà \(\widehat{ACB};\widehat{ABC}\) lần lượt là góc đối diện của cạnh AB,AC
nên \(\widehat{ACB}< \widehat{ABC}\)
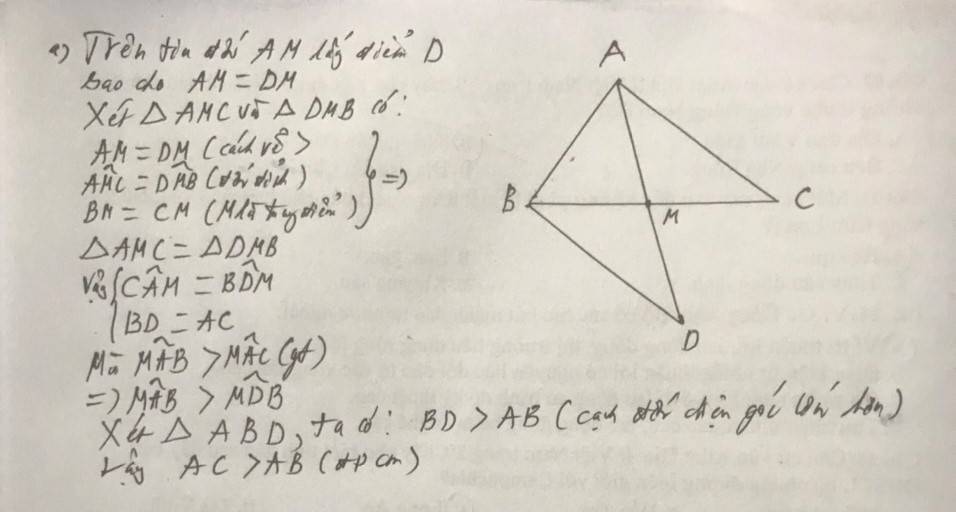
b: Trên tia đối của tia MA, lấy D sao cho MA=MD
Xét ΔMAC và ΔMDB có
MA=MD
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMDB
=>AC=BD
Ta có: ΔMAC=ΔMDB
=>\(\widehat{MAC}=\widehat{MDB}\)
=>\(\widehat{MAC}=\widehat{ADB}\)(1)
Ta có: AC=BD
AC>AB
Do đó: BD>AB
Xét ΔBAD có BD>BA
mà góc BAD,góc BDA lần lượt là góc đối diện của các cạnh BD,BA
nên \(\widehat{BAD}>\widehat{ADB}\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{MAB}>\widehat{MAC}\)

Xét tam giác AMB và tam giác AMC có:
BM = CM ( M là trung điểm BC )
góc MAB = góc MAC
Cạnh AM chung
=> tam giác AMB = tam giác AMC ( c-g-c)
=> AB=AC (2 cạnh tương ứng ) ( đpcm)
Hình bạn tự vẽ nha!
Xét tam giác MAB và tam giác MAC có:
AM là cạnh chung
Góc A1=góc A2(gt)
MB=MC(gt)
Suy ra tam giác MAB=tam giác MAC(c-g-c)
Suy ra AB=AC(hai cạnh tương ứng)
k mình nha

a: Sửa đề; ΔMAB=ΔMDC
Xét ΔMAB và ΔMDC có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔMAB=ΔMDC
b: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hbh
=>AB//CD và AB=CD<AC
=>góc CAD<góc CDA
=>góc CAD<góc BAM

a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC
CMR là gì thế bạn?