Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:tam giác ABC có góc A=90 độ
=>Tam giác ABC vuông tại A.
Ta có:AB/AC=3/4 =>AB/3=AC/4
ÁP DỤNG T/C DÃY TỈ SỐ BĂNG NHAU.TA CÓ
AB/3=AC/4=AB2+AC2/32+42=152/9+16=225/25=9
=>AB=
=>AC=
Bạn hãy tính đi nhé

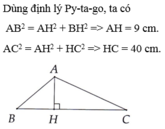
Áp dụng định lý Pi-ta-go vào tam giác vuông ABH vuông tại H ta có:
AB2= BH2 + AH2
<=> 152= 122+ AH2
<=> AH2= 152- 122= 225- 144= 81
<=> AH= 9 (cm)
Tương tự ta có : Áp dụng định lý Pi-ta-go vào tam giác vuông ACH vuông tại H .
AC2= AH2+ HC2
<=> 412= 92+ HC2
<=> HC2= 412- 92= 1681- 81= 1600
<=>HC= 40 (cm)

Bài 1: (bạn tự vẽ hình vì hình cũng dễ)
Ta có: AB = AH + BH = 1 + 4 = 5 (cm)
Vì tam giác ABC cân tại B => BA = BC => BC = 5 (cm)
Xét tam giác BCH vuông tại H có:
\(HB^2+CH^2=BC^2\left(pytago\right)\)
\(4^2+CH^2=5^2\)
\(16+CH^2=25\)
\(\Rightarrow CH^2=25-16=9\)
\(\Rightarrow CH=\sqrt{9}=3\left(cm\right)\)
Tới đây xét tiếp pytago với tam giác ACH là ra AC nhé
Bài 2: Sử dụng pytago với tam giác ABH => AH
Sử dụng pytago với ACH => AC

a,Có:\(\Delta ABC\)vuông tại A (gt)
\(\Rightarrow AB^2+AC^2=BC^2\)(Định lí Py-ta-go)
Mà AB=2cm;BC=4cm(gt)
Suy ra:\(2^2+AC^2=4^2\)
\(AC^2=8-4\)
\(AC^2=4\)
\(AC=\sqrt{4}\)
AC=2
Vậy ...
b,

bài 2:
ta có: AB<AC<BC(Vì 3cm<4cm<5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
bài 2:
ta có: AB <AC <BC (Vì 3cm <4cm <5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
HT mik làm giống bạn Dương Mạnh Quyết
AB/AC = 3/4
AB =3/4 AC
Tam giác ABC là tam giác vuông tại A
Áp dụng định lý Pytago:
AB^2 +AC^2 = BC^2
(3/4AC)^2 +AC^2 = 225
9/16 AC^2 +AC^2 =225
AC^2 x 25/16 = 225
AC^2 = 225 x16/25
AC^2 = 144 ( MÀ AC > 0)
Suy ra AC= 12
Suy ra AB/12 = 3/4
AB= 12x3/4 = 9 cm
có \(\frac{AB}{AC}=\frac{3}{4}\Rightarrow AB=\frac{3}{4}AC\) (1)
và BC = 15 cm
Tam giác ABC có góc A = 90 độ nên tam giác ABC vuông tại A
Áp dụng định lý pytago vào tam giác ABC vuông tại A:
\(AB^2+AC^2=BC^2\)(2)
thế (1) vào (2), ta được:
\(\frac{9}{16}AC^2+AC^2=225\)
\(\frac{25}{16}AC^2=225\)
\(AC^2=144\)
\(\orbr{\begin{cases}AC=12\\AC=-12\end{cases}}\)
AC = -12 (loại) vì AC \(\in\)N*
vậy AC = 12 cm
AB = 3/4.AC = 3/4 . 12 = 9 cm