Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho tam giác abc có tọa độ A(-2;3) pt đường trung tuyến BM 2x-y+1=0 và CN x+y-4=0 M,N lần lượt là trung điểm AC và AB .TÌM tọa độ B

Đáp án A
Gọi AI là đường cao kẻ từ đỉnh A của tam giác. Gọi M là trực tâm của tam giác ABC
Khi đó tọa độ điểm M thỏa mãn hệ phương trình
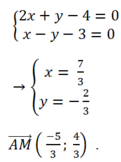
Đ ư ờ n g t h ẳ n g A I q u a M ( 7 3 ; - 2 3 ) v à n h ậ n n → ( 4 ; 5 ) l à m V T P T .
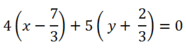
Hay 4x+ 5y – 6= 0

+) Phương trình đường cao qua B : 2x - y + 1 = 0
=> Phương trình AC có dạng : x + 2y + c = 0
Vì A ( 2; -1 ) thuộc AC => 2 + 2 ( -1 ) + c = 0 => c = 0
=> Phương trình AC: x + 2y = 0
=> Tọa độ điểm C thỏa mãn phương trình AC và đường cao qua C
nên là nghiệm của hệ pt: \(\hept{\begin{cases}x+2y=0\\3x+y+2=0\end{cases}}\)<=> C ( -4/5; 2/5)
+) Phương trình đường cao qua B : 3x + y + 2 = 0
=> Phương trình AB có dạng : x - 3y + b = 0
Vì A ( 2; -1 ) thuộc AB => 2 - 3 ( -1 ) + b= 0 => c = -5
=> Phương trình AB: x -3y -5 = 0
=> Tọa độ điểm B thỏa mãn phương trình AB và đường cao qua CB
nên là nghiệm của hệ pt: \(\hept{\begin{cases}2x-y+1=0\\x-3y-5=0\end{cases}}\)<=> C ( -8/5; -11/5)
+) M là trung điêm BC => M ( -6/5; -9/10 )
Mà A ( 2; -1)
=> \(\overrightarrow{MA}=\left(\frac{16}{5};-\frac{1}{10}\right)\)
=> MA có véc tơ pháp tuyến: ( 1/10; 16/5)
=> Viết phương trình MA : 1/10 ( x- 2 ) + 16/5 ( y+ 1 ) = 0
<=> x + 32y+ 30 = 0

Thay tọa độ A vào 2 pt trung tuyến đều không thỏa mãn
\(\Rightarrow\) 2 trung đó đó xuất phát từ B và C, giả sử trung tuyến xuất phát từ B có pt x-2y+1=0 và từ C có pt y=1
\(\Rightarrow B\left(2b-1;b\right)\) ; \(C\left(c;1\right)\)
Gọi G là trọng tâm tam giác \(\Rightarrow\) G là giao điểm 2 trung tuyến nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}x-2y+1=0\\y=1\end{matrix}\right.\) \(\Rightarrow G\left(1;1\right)\)
Áp dụng công thức trọng tâm:
\(\left\{{}\begin{matrix}1+2b-1+c=3.1\\3+b+1=3.1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2b+c=3\\b=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=-1\\c=5\end{matrix}\right.\)
\(\Rightarrow B\left(-3;-1\right)\) ; \(C\left(5;1\right)\)
Biết 3 tọa độ 3 đỉnh của tam giác, dễ dàng viết được phương trình các cạnh

1.
Tọa độ A là nghiệm: \(\left\{{}\begin{matrix}x-y+2=0\\2x-3y+1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-5\\y=-3\end{matrix}\right.\)
\(\Rightarrow A\left(-5;-3\right)\)
Phương trình BC qua B và vuông góc đường cao kẻ từ A có dạng:
\(1\left(x-2\right)+1\left(y-1\right)=0\Leftrightarrow x+y-3=0\)
Gọi M là trung điểm BC thì tọa độ M thỏa mãn:
\(\left\{{}\begin{matrix}2x-3y+1=0\\x+y-3=0\end{matrix}\right.\) \(\Rightarrow M\left(\dfrac{8}{5};\dfrac{7}{5}\right)\)
M là trung điểm BC \(\Rightarrow C\left(\dfrac{6}{5};\dfrac{9}{5}\right)\)
2.
Do C thuộc AC nên tọa độ có dạng: \(C\left(c;2c+3\right)\)
Gọi M là trung điểm BC \(\Rightarrow M\left(\dfrac{c+4}{2};\dfrac{2c+5}{2}\right)\)
M thuộc trung tuyến kẻ từ A nên:
\(\dfrac{c+4}{2}+\dfrac{2c+5}{2}-1=0\Leftrightarrow c=-\dfrac{7}{3}\)
\(\Rightarrow C\left(-\dfrac{7}{3};-\dfrac{5}{3}\right)\)

1.
Do A không thuộc hai đường trung tuyến đã cho nên giả sử đường trung tuyến xuất phát từ B, C lần lượt là \(2x-y+1=0;x+y-4=0\)
Trọng tâm G của tam giác có tọa độ là nghiệm của hệ \(\left\{{}\begin{matrix}2x-y+1=0\\x+y-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\Rightarrow G=\left(1;3\right)\)
Gọi M là trung điểm BC, ta có \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\)
\(\Rightarrow\left\{{}\begin{matrix}1+3=\dfrac{2}{3}\left(x_M+2\right)\\3-3=\dfrac{2}{3}\left(y_M-3\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_M=4\\y_M=3\end{matrix}\right.\Rightarrow M=\left(4;3\right)\)
Gọi \(N=\left(m;2m+1\right)\) là trung điểm AC \(\Rightarrow C=\left(2m+2;4m-1\right)\)
Mà C lại thuộc CG nên \(2m+2+4m-1-4=0\Rightarrow m=\dfrac{1}{2}\)
\(\Rightarrow C=\left(3;1\right)\)
Phương trình đường thẳng BC:
\(\dfrac{x-4}{3-4}=\dfrac{y-3}{1-3}\Leftrightarrow2x-y-5=0\)
2.
1.
Trọng tâm G của tam giác có tọa độ là nghiệm của hệ \(\left\{{}\begin{matrix}x-5y+1=0\\x+y-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{2}{3}\end{matrix}\right.\Rightarrow G=\left(\dfrac{2}{3};\dfrac{1}{3}\right)\)
Gọi I là trung điểm BC, ta có \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AI}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{2}{3}-1=\dfrac{2}{3}\left(x_I-1\right)\\\dfrac{1}{3}-2=\dfrac{2}{3}\left(y_I-2\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_I=\dfrac{1}{2}\\y_I=-\dfrac{1}{2}\end{matrix}\right.\Rightarrow I=\left(\dfrac{1}{2};-\dfrac{1}{2}\right)\)
Gọi \(M=\left(5m-1;m\right)\) \(\Rightarrow C=\left(10m-3;2m-2\right)\)
Mà C lại thuộc CN nên \(10m-3+2m-2-1=0\Rightarrow m=\dfrac{1}{2}\)
\(\Rightarrow C=\left(2;-1\right)\)
Phương trình đường thẳng BC:
\(\dfrac{x-2}{2-\dfrac{1}{2}}=\dfrac{y+1}{-1+\dfrac{1}{2}}\Leftrightarrow x+3y+1=0\)

Do BC vuông góc đường cao AH kẻ từ A nên BC nhận (3;4) là 1 vtpt
Phương trình BC:
\(3\left(x+4\right)+4\left(y-0\right)=0\Leftrightarrow3x+4y+12=0\)
C là giao điểm BC và trung tuyến kẻ từ C nên tọa độ C là nghiệm:
\(\left\{{}\begin{matrix}4x+y+3=0\\3x+4y+12=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=0\\y=-3\end{matrix}\right.\) \(\Rightarrow C\left(0;-3\right)\)
Gọi M là trung điểm AB \(\Rightarrow M\) thuộc trung tuyến kẻ từ C nên tọa độ M có dạng: \(M\left(m;-4m-3\right)\)
Áp dụng công thức trung điểm: \(\left\{{}\begin{matrix}x_A=2x_M-x_B=2m+4\\y_A=2y_M-y_B=-8m-6\end{matrix}\right.\)
Do A thuộc -4x+3y+2=0 nên:
\(-4\left(2m+4\right)+3\left(-8m-6\right)+2=0\Rightarrow m=-1\) \(\Rightarrow A\left(2;2\right)\)
\(\Rightarrow\overrightarrow{AB}=\left(-6;-2\right)\Rightarrow\) đường thẳng AB nhận (1;-3) là 1 vtpt
Phương trình AB:
\(1\left(x+4\right)-3\left(y-0\right)=0\Leftrightarrow x-3y+4=0\)
\(\overrightarrow{AC}=\left(-2;-5\right)\Rightarrow\) đường thẳng AC nhận (5;-2) là 1 vtpt
Phương trình AC:
\(5\left(x-2\right)-2\left(y-2\right)=0\Leftrightarrow5x-2y-6=0\)
b.
Ta có: \(\overrightarrow{AB}=\left(-6;-2\right)\Rightarrow AB=\sqrt{\left(-6\right)^2+\left(-2\right)^2}=2\sqrt{10}\)
Gọi H là chân đường cao hạ từ C xuống AB
\(\Rightarrow CH=d\left(C;AB\right)=\dfrac{\left|0-\left(-3\right).3+4\right|}{\sqrt{1^2+\left(-3\right)^2}}=\dfrac{13\sqrt{10}}{10}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}CH.AB=13\)

1.
\(\overrightarrow{OA}=\left(1;3\right)\Rightarrow OA=\sqrt{10}\)
Gọi I là trung điểm OA \(\Rightarrow I\left(\dfrac{1}{2};\dfrac{3}{2}\right)\)
Phương trình đường tròn đường kính OA nhận I là trung điểm và có bán kính \(R=\dfrac{OA}{2}=\dfrac{\sqrt{10}}{2}\):
\(\left(x-\dfrac{1}{2}\right)^2+\left(y-\dfrac{3}{2}\right)^2=\dfrac{5}{2}\)
b.
Gọi 2 trung tuyến là BN và CM (với M, N là trung điểm AB và AC)
B thuộc BN nên tọa độ có dạng: \(\left(b;1\right)\)
M là trung điểm AB \(\Rightarrow M\left(\dfrac{b+1}{2};2\right)\)
M thuộc CM nên tọa độ thỏa mãn:
\(\dfrac{b+1}{2}-4+1=0\Rightarrow b=5\Rightarrow B\left(5;1\right)\)
\(\Rightarrow\overrightarrow{AB}=\left(4;-2\right)\Rightarrow\) pt AB: \(\left\{{}\begin{matrix}x=1+2t\\y=3-t\end{matrix}\right.\)
Gọi G là trọng tâm tam giác ABC \(\Rightarrow\) G là giao điểm BN và CM
Tọa độ G thỏa mãn: \(\left\{{}\begin{matrix}y-1=0\\x-2y+1=0\end{matrix}\right.\) \(\Rightarrow G\left(1;1\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_C=3x_G-x_A-x_B=-3\\y_C=3y_G-y_A-y_B=-1\end{matrix}\right.\) \(\Rightarrow C\left(-3;-1\right)\)
Biết tọa độ C, A, B bạn tự viết pt 2 cạnh còn lại
2.
AB vuông góc với trung trực của AB nên nhận (2;-3) là 1 vtpt và (3;2) là 1 vtcp
Phương trình tham số:
\(\left\{{}\begin{matrix}x=-1+3t\\y=-3+2t\end{matrix}\right.\)
Phương trình tổng quát:
\(2\left(x+1\right)-3\left(y+3\right)=0\Leftrightarrow2x-3y-7=0\)
b. Câu này tìm trung điểm của AB hay BC nhỉ? Ta chỉ có thể tìm được trung điểm BC sau khi hoàn thành câu c (nghĩa là thứ tự bài toán bị ngược)
Gọi N là trung điểm AB \(\Rightarrow\) tọa độ N thỏa mãn:
\(\left\{{}\begin{matrix}2x-3y-7=0\\3x+2y-4=0\end{matrix}\right.\) \(\Rightarrow N\left(2;-1\right)\)
N là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}x_B=2x_N-x_A=5\\y_B=2y_N-y_A=1\end{matrix}\right.\) \(\Rightarrow B\left(5;1\right)\)
G là trọng tâm tam giác nên: \(\left\{{}\begin{matrix}x_C=3x_G-x_A-x_B=8\\y_C=3y_G-y_A-y_B=-4\end{matrix}\right.\) \(\Rightarrow C\left(8;-4\right)\)
\(\Rightarrow M\left(\dfrac{13}{2};-\dfrac{3}{2}\right)\)
Do B thuộc BH nên tọa độ có dạng \(B\left(b;2b+3\right)\)
Gọi E là trung điểm AB \(\Rightarrow E\left(\dfrac{b+1}{2};b+3\right)\)
Do E thuộc CE nên:
\(\dfrac{b+1}{2}+b+3-2=0\Rightarrow b=-1\) \(\Rightarrow B\left(-1;1\right)\)
\(\Rightarrow\overrightarrow{AB}=\left(-2;-2\right)\Rightarrow\) đường thẳng AB nhận (1;-1) là 1 vtpt
Phương trình AB:
\(1\left(x-1\right)-1\left(y-3\right)=0\Leftrightarrow x-y+2=0\)
E(x;-x+2)
Theo đề, ta có: \(\left\{{}\begin{matrix}x=\dfrac{1+x_B}{2}\\-x+2=\dfrac{3+y_B}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_B+1=2x\\y_B+3=-2x+4\end{matrix}\right.\)
=>B(2x-1;-2x+1)
vecto AB=(2x-2;-2x-2)
BH: 2x-y+3=0
=>VTPT là (2;-1)
=>VTCP là (1;2)
Theo đề, ta có: 1(2x-2)+2(-2x-2)=0
=>2x-2-4x-4=0
=>-2x-6=0
=>x=-3
=>B(5;-5)
vecto AB=(4;-8)
=>VTPT là (8;4)
Phương trình AB là:
8(x-5)+4(y+5)=0
=>2(x-5)+y+5=0
=>2x-10+y+5=0
=>2x+y-5=0