Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: Xét tứ giác AMDN có
góc AMD=góc AND=góc MAN=90 độ
AD là phan giác
=>AMDN là hình vuông
2: BC=căn 3^2+4^2=5cm
AD là phân giác
=>DB/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=5/7
=>BD=15/7cm; CD=20/7cm

chứng minh tam giác ADB đồng dạng với tam giác ABC theo trường hợp canh góc cạnh
nen góc ADB=70 =>góc bdc=110

b) Ta có: AD+DC=AC(D nằm giữa A và C)
nên DC=AC-AD=3-1=2(cm)
Ta có: DE=AD(gt)
mà AD=1cm(cmt)
nên DE=1cm
Ta có: \(\dfrac{BD}{CD}=\dfrac{\sqrt{2}}{2}\)
\(\dfrac{DE}{DB}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
Do đó: \(\dfrac{BD}{CD}=\dfrac{DE}{DB}\)\(\left(=\dfrac{\sqrt{2}}{2}\right)\)
Xét ΔBDE và ΔCDB có
\(\dfrac{BD}{CD}=\dfrac{DE}{DB}\)(cmt)
\(\widehat{BDE}\) chung
Do đó: ΔBDE\(\sim\)ΔCDB(c-g-c)
a) Ta có: AD+DE+EC=AC
mà AD=DE=EC(gt)
nên \(AD=\dfrac{AC}{3}=\dfrac{3}{3}=1\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AB^2+AD^2\)
\(\Leftrightarrow BD^2=1+1=2\)
hay \(BD=\sqrt{2}cm\)
Vậy: \(BD=\sqrt{2}cm\)

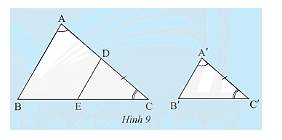
a) Vì \(ED//AB \Rightarrow \Delta DEC\backsim\Delta ABC\) (định lí)
b) Vì \(ED//AB \Rightarrow \widehat {CDE} = \widehat {CAB}\) (hai góc đồng vị)
Mà \(\widehat {CAB} = \widehat {A'}\). Do đó, \(\widehat {CDE} = \widehat {B'A'C'}\).
Xét tam giác \(A'B'C'\) và tam giác \(DEC\) ta có:
\(\widehat {B'A'C'} = \widehat {CDE}\) (chứng minh trên)
\(A'C' = CD\) (giải thuyết)
\(\widehat {C'} = \widehat C\) (giả thuyết)
Do đó, \(\Delta A'B'C' = \Delta DEC\) (g.c.g)
c) Vì tam giác \(\Delta A'B'C'\backsim\Delta DEC\) (tính chất)
Mà \(\Delta DEC\backsim\Delta ABC\) nên \(\Delta ABC\backsim\Delta A'B'C'\).

Hình vẽ:

Lời giải:
Xét tam giác $BDC$ và $ABC$ có:
$\widehat{BDC}=\widehat{ABC}$ (gt)
$\widehat{C}$ chung
$\Rightarrow \triangle BDC\sim \triangle ABC$ (g.g)
$\Rightarrow \frac{BD}{AB}=\frac{DC}{BC}=\frac{BC}{AC}$
$\Rightarrow BC^2=AC.DC=(AD+DC).DC=(7+9).9=144$
$\Rightarrow BC=12$
$\Rightarrow \frac{BD}{AB}=\frac{DC}{BC}=\frac{9}{12}=\frac{3}{4}$