Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài toán này dựa vào nhận xét sau đây: Nếu AD,BE,CF là đường cao của tam giác thì \(\frac{1}{AD}+\frac{1}{BE}+\frac{1}{CF}=\frac{1}{r}.\) Thực vậy, do tâm đường tròn nội tiếp chia tam giác ra thành 3 tam giác con có cùng độ dài đường cao là r. Do đó \(S=r\cdot\frac{AB+BC+CA}{2},\) với \(S\) là diện tích tam giác ABC. Mặt khác \(\frac{1}{AD}=\frac{BC}{2S},\frac{1}{BE}=\frac{CA}{2S},\frac{1}{CF}=\frac{AB}{2S}\to\frac{1}{AD}+\frac{1}{BE}+\frac{1}{CF}=\frac{AB+BC+CA}{2S}.\) Từ đó ta có đẳng thức.
Quay lại bài toán, từ giả thiết suy ra \(\frac{1}{AM}+\frac{1}{BN}+\frac{1}{CP}=\frac{1}{AD}+\frac{1}{BE}+\frac{1}{CF}.\) Do quan hệ giữa đường xiên và đường vuông góc, ta có \(AM\ge AD,AN\ge BE,AP\ge CF\to\)các dấu bằng phải xảy ra, do đó M,N,P trùng với chân các đường cao của tam giác. Theo tính chất của hai tiếp tuyến cắt nhau BP=BM, suy ra hai tam giác vuông AMB và CPB bằng nhau (g.c.g). Do đó AB=CB. Tương tự BC=AC. Vậy tam giác ABC đều.

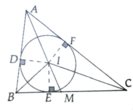
a, Áp dụng tính chất 2 tiếp tuyến tại A,B,C ta chứng minh được b + c - a 2 = AD
b, S A B C = S A I B + S B I C + S C I A
Mà ID = IE = IF = r => S A B C = p.r
c, Vì AM là phân giác của
B
A
C
^
=>
B
M
M
C
=
B
A
A
C
Áp dụng tính chất tỉ lệ thức thu được BM = a c c + b

Vẽ đường cao AH của \(\Delta\)ABC
Ta có: \(S_{MAB}=S_{MAC}=\frac{1}{2}S_{ABC}\)mà AM > AH (AH _|_ HM)
Do đó: \(\frac{4}{a}=\frac{2\cdot AH}{S_{ABC}}\le\frac{2AM}{S_{ABC}}=\frac{AM}{S_{MAB}}\left(1\right)\)
Gọi I là tâm đường tròn nội tiếp \(\Delta\)ABC
Ta có \(S_{ABC}=S_{IBC}+S_{IAC}+S_{IAB}\)
\(\Rightarrow S_{ABC}=\frac{r\cdot BC}{2}+\frac{r\cdot AC}{2}+\frac{r\cdot AB}{2}\)
\(\Rightarrow\frac{2}{r}=\frac{AB+BC+AC}{2S_{MAB}}\)
Tương tự xét \(\Delta\)MAB và \(\Delta\)MAC ta cũng có:
\(\hept{\begin{cases}\frac{2}{r_1}=\frac{AM+AB+\frac{BC}{2}}{S_{MAB}}\\\frac{2}{r_2}=\frac{AM+AC+\frac{BC}{2}}{A_{MAC}}\end{cases}\left(2\right)}\)
Do đó:
\(\frac{4}{a}+\frac{2}{r}\le\frac{MA}{S_{MAB}}+\frac{AB+BC+AC}{2S_{MAB}}=\frac{1}{2}\left(\frac{AM}{S_{MAB}}+\frac{AB+\frac{AC}{2}}{S_{MAB}}\right)+\frac{1}{2}\left(\frac{AM}{S_{MAC}}+\frac{AC+\frac{BC}{2}}{S_{MAC}}\right)=\frac{1}{r_1}+\frac{1}{r_2}\)
Vậy \(\frac{1}{r_1}+\frac{1}{r_2}\ge2\left(\frac{1}{r}+\frac{1}{a}\right)\)

BÀI LÀM
a, xét tứ giác ADOE có:
góc A= góc E=góc D=90O
mà ta thấy: OE=OD( bán kính = nhau)
vậy tứ giác ADOE là hình vuông (dhnb)
a) Dễ thấy tứ giác AEOD là hình chữ nhật (tứ giác có 3 góc vuông).
Mà OD = OE ( cùng bằng bán kính đường tròn nội tiếp tam giác ABC).
Nên tứ giác AEOD là hình vuông.
b) Gọi H là chân đường vuông góc kẻ từ O xuống BC.
Có SΔABC=SΔOAB+SΔOBC+SΔOAC
=12 OD.AB+12 OE.AC+12 OH.BC
=12 r.(AB+AC+BC)
=12 pr ( là chu vi của tam giác , là bán kính đường tròn nội tiếp).
c) Áp dụng định lý Pi-ta-go ta có: BC=√AB2+AC2=10(cm).
Diện tích tam giác ABC là: 12 AB.AC=12 .6.8=24(cm2).
Chu vi tam giác ABC là: 6+8+10=24(cm).
Suy ra: 24=12 .24.r⇔r=2(cm).
a) Gọi tâm của đường tròn nội tiếp \(\Delta\)ABC là I. (I) tiếp xúc với BC,CA,AB tại D,E,F
Ta có \(S_{BIC}=\frac{1}{2}ID.BC=r.\frac{BC}{2}\). Tương tự \(S_{CIA}=r.\frac{CA}{2};S_{AIB}=r.\frac{AB}{2}\)
Vậy \(S_{ABC}=r.\frac{BC+CA+AB}{2}=pr\)(đpcm).
b) Đặt \(BC=a,CA=b,AB=c,AM=m_A,BM=m_B,CM=m_C\)
Áp dụng công thức tính đường trung tuyến có \(m_A=\frac{\sqrt{2\left(b^2+c^2\right)-a^2}}{2}\)
\(\Rightarrow\frac{1}{m_A}=\frac{2}{\sqrt{2\left(b^2+c^2\right)-a^2}}\), Hoàn toàn tương tự đối với \(m_B,m_C\)
Từ đó \(\frac{1}{m_A}+\frac{1}{m_B}+\frac{1}{m_C}=\frac{2}{\sqrt{2\left(b^2+c^2\right)-a^2}}+\frac{2}{\sqrt{2\left(c^2+a^2\right)-b^2}}+\frac{2}{\sqrt{2\left(a^2+b^2\right)-c^2}}\)
Lại có \(r=\frac{S}{p}=\frac{\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}}{p}=\sqrt{\frac{\left(p-a\right)\left(p-b\right)\left(p-c\right)}{p}}\)(Công thức Heron)
\(=\frac{\sqrt{\left(b+c-a\right)\left(c+a-b\right)\left(a+b-c\right)}}{2\sqrt{a+b+c}}\)
Kết hợp với giả thiết \(\frac{1}{m_A}+\frac{1}{m_B}+\frac{1}{m_C}=\frac{1}{r}\) suy ra:
\(\frac{1}{\sqrt{2\left(b^2+c^2\right)-a^2}}+\frac{1}{\sqrt{2\left(c^2+a^2\right)-b^2}}+\frac{1}{\sqrt{2\left(a^2+b^2\right)-c^2}}\)
\(=\frac{\sqrt{a+b+c}}{\sqrt{\left(b+c-a\right)\left(c+a-b\right)\left(a+b-c\right)}}\)(1)
Áp dụng BĐT Cauchy: \(VT_{\left(1\right)}\le\frac{1}{\sqrt{\left(b+c\right)^2-a^2}}+\frac{1}{\sqrt{\left(c+a\right)^2-b^2}}+\frac{1}{\sqrt{\left(a+b\right)^2-c^2}}\)
\(=\frac{1}{\sqrt{a+b+c}}.\frac{\sqrt{\left(a+b-c\right)\left(b+c-a\right)}+\sqrt{\left(b+c-a\right)\left(c+a-b\right)}+\sqrt{\left(c+a-b\right)\left(a+b-c\right)}}{\sqrt{\left(b+c-a\right)\left(c+a-b\right)\left(a+b-c\right)}}\)\(\le\frac{1}{\sqrt{a+b+c}}.\frac{a+b+c}{\sqrt{\left(b+c-a\right)\left(c+a-b\right)\left(a+b-c\right)}}\)
\(=\frac{\sqrt{a+b+c}}{\sqrt{\left(b+c-a\right)\left(c+a-b\right)\left(a+b-c\right)}}=VP_{\left(1\right)}\)
Dấu "=" xảy ra khi và chỉ khi \(a=b=c\)<=> \(\Delta\)ABC đều (đpcm).