Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Có: AB = AC (GT)
=> Tam giác ABC cân tại A
Xét tam giác ABM và tam giác ACM:
AB = AC (GT)
Góc B = Góc C (Tam giác ABC cân tại A)
BM = CM (GT)
=> Tam giác ABM = Tam giác ACM (c - g - c)
b) Tam giác ABM = Tam giác ACM (cmt)
=> Góc BAM = Góc CAM (2 góc tương ứng)
=> AM là phân gicacs của góc BAC
c) Tam giác ABM = Tam giác ACM (cmt)
=> Góc AMB = Góc AMC (2 góc tương ứng)
Mà 2 góc này là 2 góc kề bù
=> Góc AMB = Góc AMC = 180 độ : 2 = 90 độ
=> AM vuông góc với BC
a) Có: AB = AC (GT)
=> Tam giác ABC cân tại A
Xét tam giác ABM và tam giác ACM:
AB = AC (GT)
Góc B = Góc C (Tam giác ABC cân tại A)
BM = CM (GT)
=> Tam giác ABM = Tam giác ACM (c - g - c)
b) Tam giác ABM = Tam giác ACM (cmt)
=> Góc BAM = Góc CAM (2 góc tương ứng)
=> AM là phân gicacs của góc BAC
c) Tam giác ABM = Tam giác ACM (cmt)
=> Góc AMB = Góc AMC (2 góc tương ứng)
Mà 2 góc này là 2 góc kề bù
=> Góc AMB = Góc AMC = 180 độ : 2 = 90 độ
=> AM vuông góc với BC

b: Ta có: ΔBAC cân tại A
mà AM là đường cao
nên M là trung điểm của BC

a: Sửa đề: ΔABM=ΔACM
Xét ΔABM và ΔACM có
AB=AC
MB=MC
AM chung
Do đó: ΔABM=ΔACM
b: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
=>AM là phân giác của \(\widehat{BAC}\)
c: AB=AC
MB=MC
Do đó: AM là đường trung trực của BC
=>AM\(\perp\)BC

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó:ΔABM=ΔACM
b: Ta có: ΔABM=ΔACM
nên \(\widehat{BAM}=\widehat{CAM}\)
hay AM là tia phân giác của \(\widehat{BAC}\)
c: Ta có: AB=AC
nên A nằm trên đường trung trực của BC(1)
Ta có: MB=MC
nên M nằm trên đường trung trực của BC(2)
từ (1) và (2) suy ra AM là đường trung trực của BC

1: Xét ΔABC có AB=AC
nên ΔABC cân tại A
hay \(\widehat{B}=\widehat{C}\)

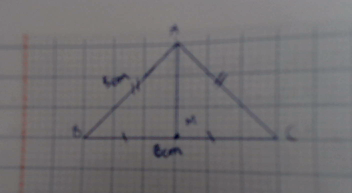 cam máy tính hình nó mờ nha bạn
cam máy tính hình nó mờ nha bạn
a) Xét ΔAMB và ΔAMC ta có:
AB=AC ( tích chất tam giác cân)
AM=MC (giả thiết)
AM cạnh chung
⇒ ΔAMB = ΔAMC (c-c-c)
⇒ \(\widehat{AMB}=\widehat{AMC}\) (hai góc tương ứng), mà hai góc này kề bù nên
\(\widehat{AMB}=\widehat{AMC}=\dfrac{180}{2}=90^o\)
Vậy AM ⊥ BC (đpcm)
b) từ câu a ta có ΔAMB = ΔAMC nên:
\(\widehat{BAM}=\widehat{CAM}\) (hai góc tương ứng)
⇒ AM là tia phân giác của \(\widehat{BAC}\) (đpcm)
c) Ta có AM ⊥ BC (1)
BM=CM (2) vì AM vuông góc với BC và M cách đều BC (BM=CM)
từ (1) và (2) ⇒ AM là đường trung trực của AB

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác
a) Xét tam giác ABM và tam giác ACM:
+ AM chung.
+ AB = AC (gt).
+ MB = MC (M là trung điểm của BC).
\(\Rightarrow\) Tam giác ABM = Tam giác ACM (c - c - c).
b) Xét tam giác ABC: AB = AC (gt).
\(\Rightarrow\) Tam giác ABC cân tại A.Mà AM là trung tuyến (M là trung điểm của BC).\(\Rightarrow\) AM là tia phân giác của góc BAC (Tính chất tam giác cân).