Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
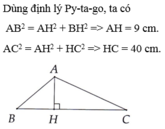
Áp dụng định lý Pitago:
$32=BH^2=AB^2-AH^2$
$CH^2=AC^2-AH^2=81-AH^2$
$\Rightarrow CH^2-32=81-AB^2$
hay $CH^2-32=81-(BC^2-AC^2)=81-(BC^2-81)=162-BC^2$
hay $CH^2=194-BC^2=194-(\sqrt{32}+CH)^2$
$2CH^2+2\sqrt{32}CH+32=194$
$2CH^2+2\sqrt{32}CH-162=0$
$\Rightarrow CH=\sqrt{89}-2\sqrt{2}$ (do $CH>0$)
$\Rightarrow BC=CH+BH=\sqrt{89}-2\sqrt{2}+\sqrt{32}\sqrt{89}+2\sqrt{2}$

Xét tam giác IMB và tam giác HMC có :
góc BIM = góc CHM ( = 90 độ )
MI = MH (gt)
góc IMB = góc HMC ( đối đỉnh )
=> Tam giác IMB = tam giác HMC ( g-c-g )
=> MB = MC và góc IBM = góc HCM (1)
Xét tam giác MBC có : MB = MC (cmt)
=> Tam giác MBC cân tại M
=> góc MBC = góc MCB (2)
Từ (1) và (2) => góc ABC = góc ACB
Xét ta giác ABC có : góc ABC = góc ACB (cmt)
=> Tam giác ABC cân tại A (đpcm)
Vẽ hình khó quá nên mk xin phép k vẽ nha ^^
M là giao của 2 đường cao BH và CI của tam giác ABC => M là trực tâm của tam giác ABC.
=> AM vuông góc với BC.
Xét tam giác AMI vuông tại I và tam giác AMH vuông tại H có
AM chung
MI = MH( gt)
=> \(\Delta AMI=\Delta AMH\)(cạnh huyền - cạnh góc vuông)
=> \(\widehat{IAM}=\widehat{HAM}\)=> AM là phân giác góc BAC.
Tam giác ABC có AM là đường phân giác, vừa là đương cao => Tam giác ABC cân tại A( đpcm)