Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xet ΔEBD vuông tại E và ΔFCD vuông tại F có
BD=CD
góc B=góc C
=>ΔEBD=ΔFCD
b: Xet ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
DE=DF
=>ΔAED=ΔAFD

a, xét tam giác DEB và tam giác DFC có : góc BED = góc DFC = 90
BD = DF do D là trung điểm của BC (gt)
góc ABC = góc ACB do tam giác ABC cân tại A (gt)
=> tam giác DEB = tam giác DFC (ch-gn)
b, tam giác DEB = tam giác DFC (Câu a)
=> DE = DF (đn)
xét tam giác ADE và tam giác ADF có : AD chung
góc AED = tam giác AFD = 90
=> tam giác ADE = tam giác ADF (ch-cgv)
c, tam giác ADE = tam giác ADF (câu b)
=> góc BAD = góc CAD (đn)
AD nằm giữa AB và AC
=> AD là phân giác của góc BAC (Đn)
( Hình vẽ không được chính xác lắm mong bạn thông cảm )
a) Ta có \(\Delta ABC\) cân tại A \(\Rightarrow\widehat{B}=\widehat{C}\) ( tính chất )
Do \(D\) là trung điểm của BC
\(\Rightarrow BD=CD=\frac{BC}{2}\)
Xét \(\Delta DEB\) và \(\Delta DFC\) có :
\(\hept{\begin{cases}\widehat{DEB}=\widehat{DFC}\left(=90^o\right)\\BD=CD\left(cmt\right)\\\widehat{EBD}=\widehat{FCD}\left(cmt\right)\end{cases}}\)
\(\Rightarrow\)\(\Delta DEB\)\(=\)\(\Delta DFC\) ( cạnh huyền - góc nhọn )
b) Do \(\Delta DEB=\Delta DFC\left(cmt\right)\)
\(\Rightarrow DE=DF\)
Xét \(\Delta AED\) và \(\Delta AFD\) có :
\(\hept{\begin{cases}\widehat{DEA}=\widehat{DFA}\left(=90^o\right)\\ADchung\\DE=DF\left(cmt\right)\end{cases}}\)
\(\Rightarrow\Delta AED=\Delta AFD\) ( cạnh huyền - cạnh góc vuông )
c) Từ \(\Rightarrow\Delta AED=\Delta AFD\) (cmt)
\(\Rightarrow\widehat{EAD}=\widehat{FAD}\Rightarrow\widehat{BAD}=\widehat{CAD}\)
\(\Rightarrow AD\) là tia phân giác của \(\widehat{BAC}\)

Xét 2 tam giác DEB và DFC:
.\(\widehat{E}\)=\(\widehat{F}\) (gt)
.\(\widehat{B}\)=\(\widehat{C}\) (gt)
.BD = DC (gt)
\(\Rightarrow\)Tam giác DEB bằng tam giác DFC. (g.c.g)
b Xét hai tam giác AED và ADF.
.\(\widehat{E}\)=\(\widehat{F}\)(gt)
.Chung cạnh AD
.\(\widehat{A1}\)=\(\widehat{A2}\)(gt)
\(\Rightarrow\)Tam giác AED =ADF (g c g)
c Xét hai tam giác ABD và ACD
\(\widehat{B}\)=\(\widehat{C}\)(gt)
. BA = BC (gt)
..BD= DC (gt)
\(\Rightarrow\)Tam giác ABD = ACD (c.g.c)
\(\Rightarrow\)Hai tam giác này phải chung cạnh AD mà : \(\Delta\)ABD=\(\Delta\)ACD =\(\Delta\)ABC:2
\(\Rightarrow\)ADlà tia phân giác của BAC

a: Xét ΔABD và ΔACD co
AB=AC
BD=CD
AD chung
=>ΔABD=ΔACD
b: ΔABD=ΔACD
=>góc BAD=góc CAD
=>AD là phân giác của góc BAC
c: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
góc EAD=góc FAD
=>ΔAED=ΔAFD
d: Xét ΔDEB vuông tại E và ΔDFC vuông tại F có
DB=DC
DE=DF
=>ΔDEB=ΔDFC

a. lỗi
b. Xét tam giác ABD và tam giác ACD:
AB = AC (tam giác ABC cân tại A)
AD chung
BD = CD ( D là trung điểm BC)
=> tam giác ABD = tam giác ACD (c-c-c)
=> góc BAD = góc CAD (2 góc tương ứng)
Xét tam giác AED và tam giác AFD:
AED = AFD (DE ⊥ AB
DF ⊥ AC)
góc BAD = góc CAD (cmt)
AD chung
=> tam giác AED và tam giác AFD (ch-gn) (đpcm)

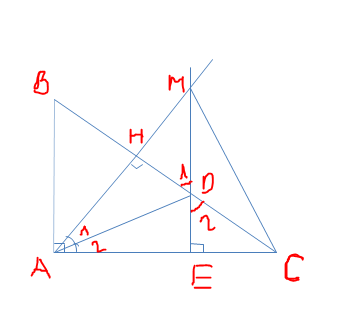
a/ Xét \(\Delta\) vuông AHD và \(\Delta\) AED. Có:
\(\widehat{A1}\)= \(\widehat{A2}\) ( giả thiết)
AD chung
=> \(\Delta AHD=\Delta AED\) ( ch-gn)
=> DH = DE ( 2 cạnh tương ứng )
b/ BMC không cân được bạn nhé. bạn chép nhầm đề bài r: Chứng minh DMC cân mới đúng.
Xét \(\Delta vuôngHDM\) và \(\Delta vuôngEDC\). Có:
\(\widehat{D1}\) = \(\widehat{D2}\) ( đối đỉnh)
HD = HE ( cmt)
=> \(\Delta HDM=\Delta EDC\left(cgv-gnk\right)\)
=> DM = DC ( 2 cạnh tương ứng)
=> Xét \(\Delta DMCcóDM=DC=>\Delta DMCcân\left(cântạiD\right)\)
~ Cậu ktra lại nhé~

a: Xét ΔEBD vuông tại E và ΔFCD vuông tại F có
BD=CD
\(\widehat{B}=\widehat{C}\)
Do đó: ΔEBD=ΔFCD
Suy ra: EB=FC
b: Ta có: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là trung trực của BC
c: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
DE=DF
Do đó: ΔAED=ΔAFD
d: Xét ΔABC có AE/AB=AF/AC
nên EF//BC

a: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
góc EAD=góc FAD
=>ΔAED=ΔAFD
=>AE=AF và DE=DF
=>AD là trung trực của EF
b: Sửa đề: ΔEKF
Xét ΔEKF có
FD là trung tuyến
FD=EK/2
=>ΔFEK vuông tại F

a: Xét ΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔABD=ΔACD