Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét ΔABC có AD là đường phân giác
->\(\dfrac{AB}{BO}=\dfrac{AC}{OC}\)
áp dụng dãy tỉ số bằng nhau ta có
\(\dfrac{AB}{BO}=\dfrac{AC}{OC}=\dfrac{AB+AC}{BO+DO}=\dfrac{AC+AB}{BC}hay\dfrac{6}{BO}=\dfrac{10}{OC}=\dfrac{10+6}{8}=2\)
suy ra: \(BO=\dfrac{6}{2}=3\left(cm\right)\)
\(CO=\dfrac{10}{2}=5\left(cm\right)\)
cho tam giác nhọn abc o thuộc tam giác có OA,OB,OC cắt BC, CA, AB tại D,E,F. CMR AO/AD+OB/BE+OC/CF=2


Tự vẽ hình.
a) Xét tam giác OAB có AB // CD
⇒AOOC=OBOD=ABDC⇒12OC=93=18DC⇒AOOC=OBOD=ABDC⇒12OC=93=18DC ( Hệ quả định lý Ta - lét ) (1)
=> OC = 4cm, DC = 6cm
Vậy OC = 4cm và DC = 6cm
b) Xét tam giác FAB có DC // AB
⇒FDAD=FCCB⇒FD.BC=FC.AD⇒FDAD=FCCB⇒FD.BC=FC.AD ( ĐPCM )
c) Theo (1), ta đã có:
OAOC=OBOD⇒OAOA+OC=OBOB+OD⇒OAAC=OBBDOAOC=OBOD⇒OAOA+OC=OBOB+OD⇒OAAC=OBBD (2)
Vì MN // AB mà AB // DC => MN // DC
Xét tam giác ADC có MO// DC
⇒MODC=AOAC⇒MODC=AOAC ( Hệ quả định lý Ta - lét ) (3)
CMTT : ONDC=OBDBONDC=OBDB (4)
Từ (2), (3) và (4) => MODC=NODC⇒MO=NOMODC=NODC⇒MO=NO ( ĐPCM )

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
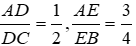


Chắc lớp 6 chưa học đến quá khó đâu , mình làm cách mang tính trực quan nhé
Ta có lục giác đều ABCDEG có các góc tạo bởi 2 cạnh kề nhau là 120 độ.
Khi lấy giao điểm O của các đường chéo đã chia hình thành 6 tam giác cân tại O và có góc ở đáy là 120: 2 =60 độ
Nên các tam giác AOB.BOC,COD,DOE,EOG,GOA là tam giác đều
=> AO=BO=CO=DO=OE=OG