Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

vì m là trung điểm nên bm=cm
vì am chung và theo gt ab=ac nên tam giác abm=acm
góc a =40 độ suy ra góc mab = góc mac=20
vì góc amb+amc=180độ mà góc amb=amc nên amb=amc=90 độ (2 góc tương ứng)
suy ra góc abm=góc acm =70 độ
vậy góc a= c =70 độ
góc amb=amc=90 độ
góc cam=bam=20 độ

Đáp án:
ΔAMB: ∠B = 70o70o; ∠AMB = 90o90o; ∠BAM = 20o20o
ΔAMC: ∠C = 70o70o; ∠AMC = 90o90o; ∠CAM = 20o20o
Giải thích các bước giải:
ΔABC có AB = AC ⇔ ΔABC cân tại A ⇔ ∠B = ∠C
Mà ∠BAC = 40o40o ⇒ ∠B + ∠C = 140o140o
⇒ ∠B = ∠C = 70o70o
Xét ΔAMB và ΔAMC có:
AB = AC (gt)
AM: cạnh chung
MB = MC (M là trung điểm của BC)
⇒ ΔAMB = ΔAMC (c.c.c)
⇒ ∠AMB = ∠AMC (2 góc tương ứng)
∠BAM = ∠CAM (2 góc tương ứng)
Lại có: ∠AMB + ∠AMC = 180o180o (2 góc kề bù)
⇒ ∠AMB = ∠AMC = 180o2180o2 = 90o90o
∠BAM + ∠CAM = ∠BAC = 40o40o
⇒ ∠BAM = ∠CAM = 40o240o2 = 20o20o

Giải nề
A) xét ∆ amb và ∆ amc
Có AM chung
BM =MC ( M là trung điểm BC)
AB =AC (gt)
=> ∆ amb = ∆ amc ( c.c.c)
B) ∆ ABC có
AB = AC ( gt)
Nên ∆ ABC cân tại a
Có AM là trung tuyến
Nên cũng là đường cao
=> AM là đường trung trực của BC
C) ta có ∆ ABC là tam giác cân
Nên AM cũng là phân giác
=>Góc BAM = góc CAM = 1/2 góc bác = 25°
Ta có AM là đường cao
Hay AM vuông góc với BC
=> Góc AMB = 90°
Vì là ∆ vuông nên
Góc B = 90° -góc BAM
Góc B = 65°
Vậy ... Kết luận các câu trên nữa nha

tam giác ABM và tam giác ACM có: AB = AC (GT) góc ABM = góc ACM (vì AB = AC => tam giác ABC cân) BM = MC (GT) => tam giác ABM = tam giác ACM (c.g.c) => ˆ A M B = ˆ A M C (2 góc tương ứng) Mà ˆ A M B + ˆ A M C =1800 (kề bù) => ˆ A M B = ˆ A M C = 1 2 1800 = 900 Vậy ˆ A M B =900 ; ˆ A M C =900

Ta có AB = AC \(\Rightarrow\) tam giác ABC cân tại A
\(\Rightarrow\) góc B = góc C = (180 - góc A) : 2 = 70 độ
Tam giác ABC cân tại A có đường trung tuyến AM (M là trung điểm của BC) còn là đường cao
nên góc AMB = góc AMC = 90 độ

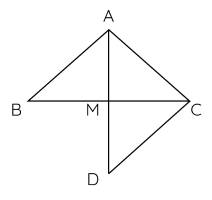
a) Xét hai tam giác $AMB$ và $AMC$ có:
$AM$ là cạnh chung;
$AB = AC$ (gt);
$BM = MC$ ($M$ là trung điểm $BC$);
Suy ra $\Delta AMB=\Delta AMC$ (c.c.c)
b) $\Delta AMB=\Delta AMC$ suy ra
$\widehat{BAM} = \widehat{CAM}$ (hai góc tương ứng)
Suy ra $AM$ là tia phân giác của góc $BAC$.
c) Xét hai tam giác $AMD$ và $DMC$ có:
$AM = AD$ (gt);
$\widehat{AMB} = \widehat{CMD}$ (hai góc đối đỉnh);
$BM = MC$.
Nên $\Delta AMD=\Delta DMC$ (c.g.c)
Suy ra $\widehat{BAM} = \widehat{CDM}$ (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong nên $AB$ // $CD$.
Vì AB=AC nên tam giác ABC là tam giác cân tại A , có góc B = góc C
Vì M là trung điểm của BC nên : AM là đường trung tuyến của tam giác ABC nên AM sẽ vuông góc với BC
=>AMB=AMC
AMB+AMC=1800 ( 2 óc kề bù )
2AMB=1800
AMC=900=AMB
A+B+C=1800
400+2B=1800
2B=1400
B=700=C
Vì AM là đường trung tuyến của góc A nên :
BAM=CAM
BAM+CAM=ABC
BAM+CAM=400
2BAM=400
BAM=200=CAM
Vậy trong tam giác AMB , có Góc BAM =200, góc ABM = 700 , góc AMB=900
trong tam giác AMC , có Góc CAM =200, góc ACM = 700 , góc AMC=900