Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

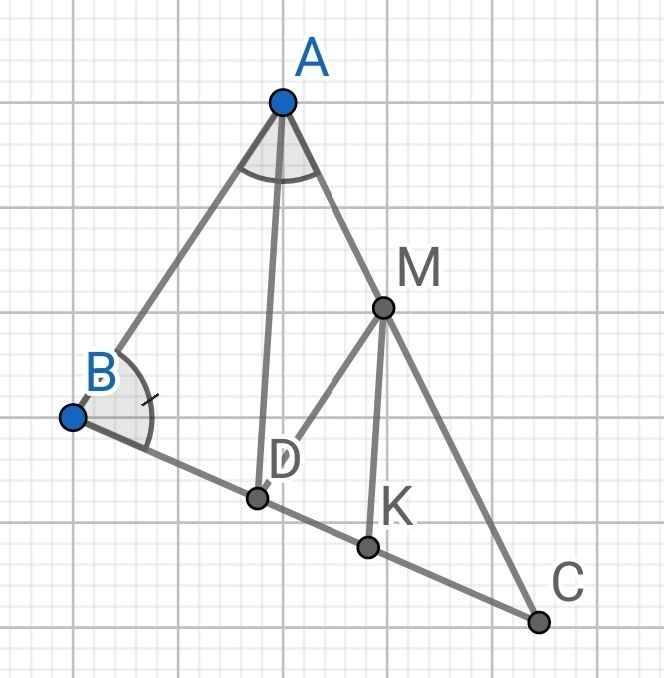
Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠DAM = 60⁰ : 2 = 30⁰
Do DM // AB (gt)
⇒ ∠ADM = ∠BAD = 30⁰ (so le trong)
Do DM // AB (gt)
⇒ ∠MDK = ∠B = 80⁰ (đồng vị)
⇒ ∠ADK = ∠ADM + ∠MDK
= 30⁰ + 80⁰
= 110⁰

Không mất tính tổng quát. g/s : AC>AB
Trên đoạn AB lấy F sao cho AE=AF
Xét tam giác AED và tam giác AFD có:
AE=AF
AD chunh
^EAD=^FAD ( DA là phân giác góc A)
=> Tam giác AED =Tam giác FFD
=> DE=DF (1)
Ta lại có:
^DFB =^DAF+^ADF =^DAE+^ADE=^CED ( các cặp góc bằng nhau, tính chất góc ngoài của tam giác)
=> ^DFB=^CED
mà ^CED=^CBA ( cùng phụ góc ECD)
=> ^DFB=^CBA
=> Tam giác DFB cân
=> DF=DB (2)
Từ (1) , (2) => DE=DB và ED vuông BD
=> Tam giác BDE vuông cân
b) Tam giác BDE vuông cân
=> ^^DBE=^DEB=45^o
+)Xét tam giác AEB có: ^EAB =90^o; ^BEA=^BCE+^CBE=^ACB+^DBE=30^o+45^o=75^o (tính chất góc ngoài)
=> ^EBA=90^o-^EAB=90^o-75^o=15^o
+)Xét tam giác CED vuông tại D có góc C bằng 30 độ
=> CE=2ED=\(2\sqrt{3}\)
Áp dụng định lí pitago
CD^2=CE^2-ED^2=9 => CD=3
Tam giác EDB vuông cân
\(DB=DE=\sqrt{3}\)
Áp dụng định li pitago
\(EB^2=DB^2+DE^2=6\Rightarrow EB=\sqrt{6}\)
Trog tam giác BEC có: \(EC=2\sqrt{3};BC=3+\sqrt{3};BE=\sqrt{6}\)

\(a,\widehat{A}+\widehat{B}+\widehat{C}=180\\ \Rightarrow180-3\widehat{C}+\widehat{C}+70=180\\ \Rightarrow-2\widehat{C}=-70\\ \Rightarrow\widehat{C}=35\\ \Rightarrow\widehat{A}=180-35=145\)

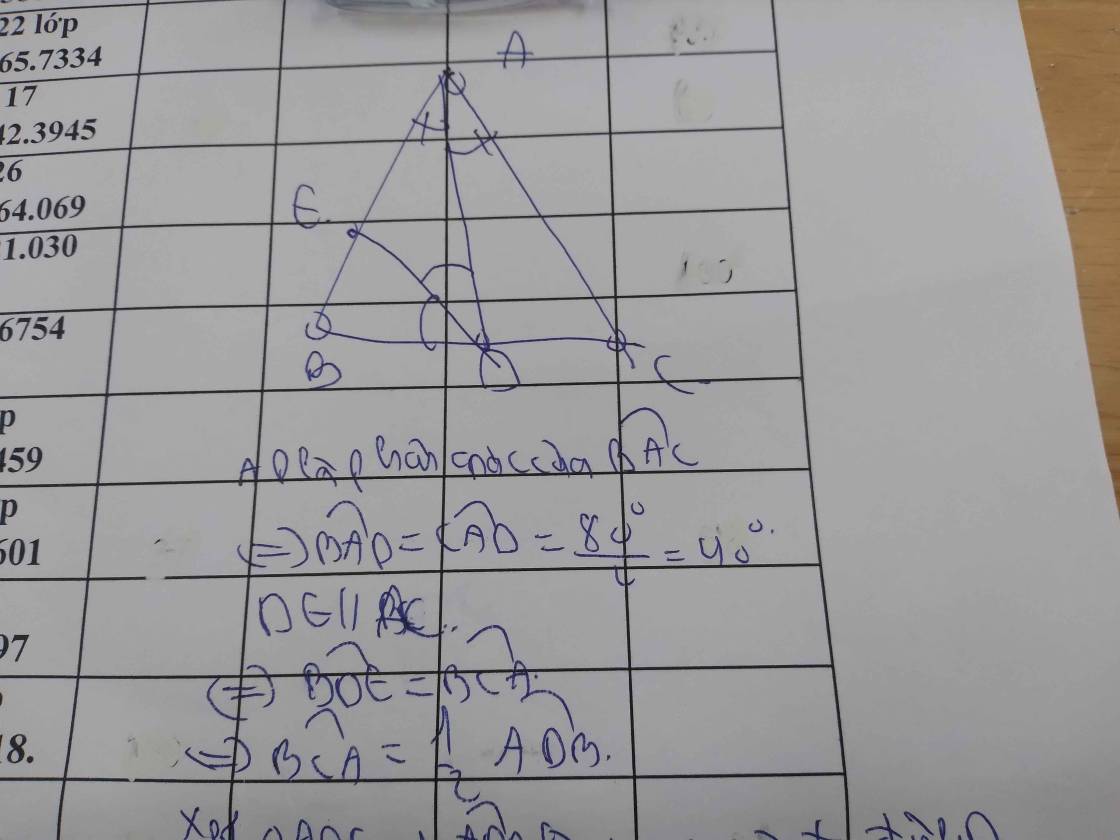
a) Xét tam giác ABC. Ta có:
Vì AD là tia phân giác của góc A nên:
\(\widehat{BAD}=\widehat{DAC}=\frac{\widehat{A}}{2}=40^{^o}\)
\(\widehat{ADB}=180^o-70^o-40^o=70^o\)
Vì \(\widehat{ADB}=\widehat{ABD}=70^o\)nên ABD là tam giác cân.
b)Vì \(\widehat{ADB}\)kề bù với \(\widehat{ADC}\)nên \(\widehat{ADC}=180^o-70^o=110^o\)
Do tam giác ACD là tam giác nên \(\widehat{ACD}=180^o-40^o-110^o=30^o\)
c) Đặt đỉnh ngoài của B là B1.
Ta có: \(\widehat{B_1}=180^o-70^o=110^o\)
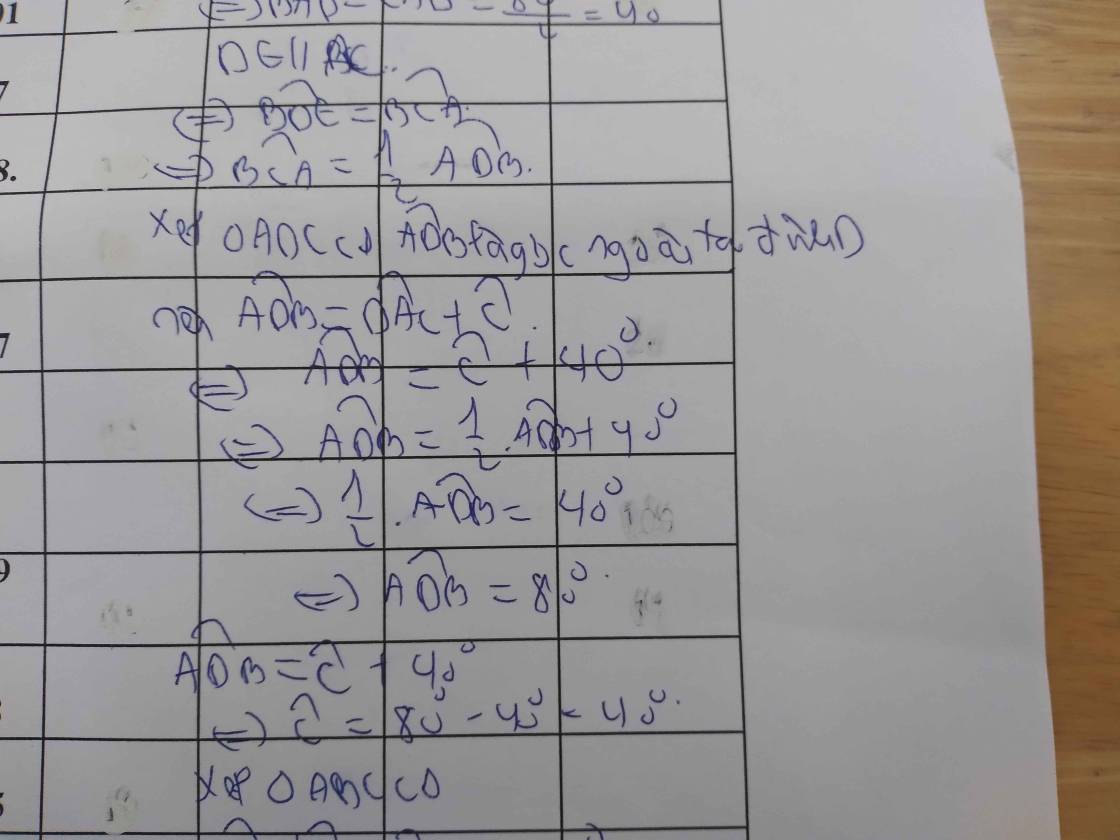
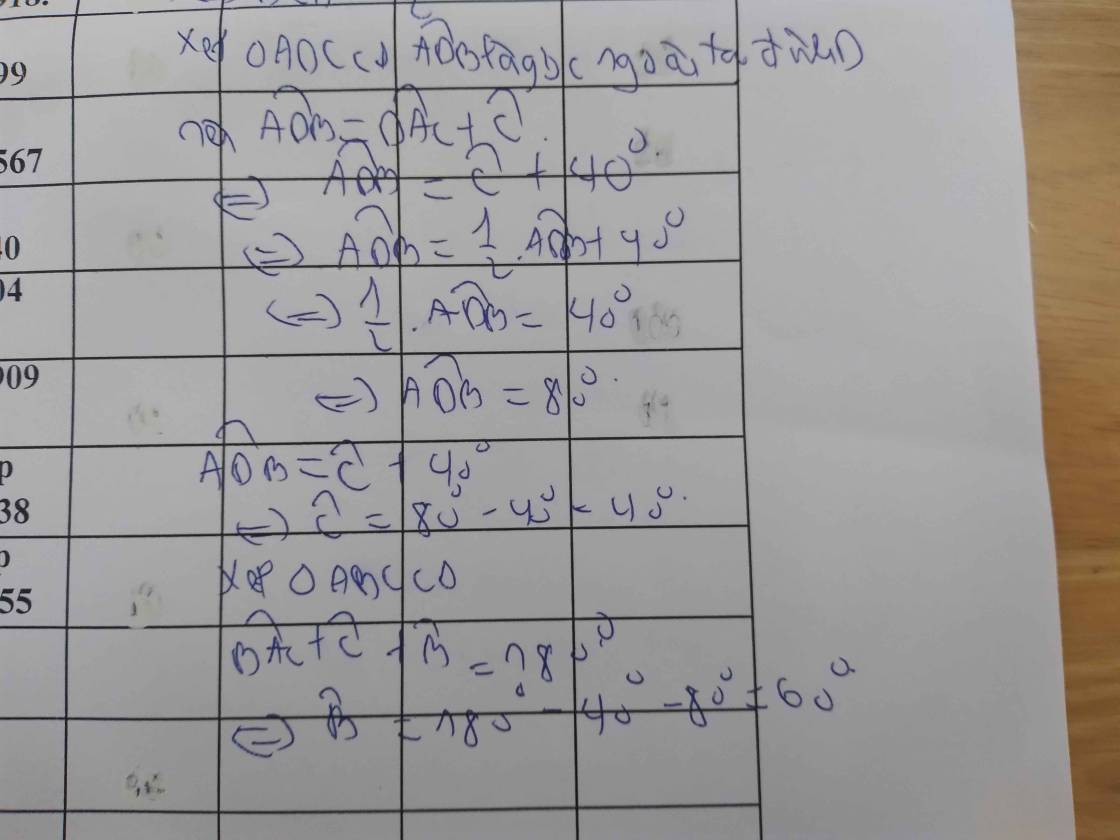
ADB=100o
ADC=80o
BAD=40o
CAD=40o
ACD= 60o
ABD= 40o