Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha![]()
AD = AB + BD
AE = AC + CE
mà AB = AC (tam giác ABC cân tại A)
BD = CE (gt)
=> AD = AE
HAE = HAB + BAE
KAD = KAC + CAD
mà HAB = KAC (tam giác AHB = tam giác AKC)
=> HAE = KAD
Xét tam giác AHE và tam giác AKD có:
AD = AE (chứng minh trên)
HAE = KAD (chứng minh trên)
AH = AK (tam giác AHB = tam giác AKC)
=> Tam giác AHE = Tam giác AKD (c.g.c)
Chúc bạn học tốt![]()

Bạn tự vẽ hình nha![]()
AD = AB + BD
AE = AC + CE
mà AB = AC (tam giác ABC cân tại A)
BD = CE (gt)
=> AD = AE
HAE = HAB + BAE
KAD = KAC + CAD
mà HAB = KAC (tam giác AHB = tam giác AKC)
=> HAE = KAD
Xét tam giác AHE và tam giác AKD có:
AD = AE (chứng minh trên)
HAE = KAD (chứng minh trên)
AH = AK (tam giác AHB = tam giác AKC)
=> Tam giác AHE = Tam giác AKD (c.g.c)
Chúc bạn học tốt![]()
a) Xét ΔΔvuông HBD và ΔΔvuông KCE, có:
BD=CE (gt)
B1ˆB1^=B2ˆB2^ (đối đỉnh)
C1ˆC1^=C2ˆC2^(đối đỉnh)
Mà B1ˆB1^=C1ˆC1^(gt)
nên B2ˆB2^=C2ˆC2^
Do đó:ΔΔ HBD = ΔΔKCE (c.h-g.n)
=>HB=CK (2 cạnh tương ứng)
b)Xét ΔΔAHB và ΔΔAKC có:
HB=CK (c/m trên)
AB=AC (gt)
ABHˆABH^=ACKˆACK^ (vì ABHˆABH^=1800-B1ˆB1^ ; ACKˆACK^=180o-C1ˆC1^ mà B1ˆB1^=C1ˆC1^)
c)
Do đó: ΔΔAHB = ΔΔAKC (c-g-c)
=>AHBˆAHB^=AKCˆAKC^ (2 góc tương ứng)

a, Vì \(\Delta ABC\) cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}\Rightarrow\widehat{HBD}=\widehat{KCE}\) ( vì là các góc đối đỉnh )
Xét hai tam giác vuông là \(\Delta HBD\) và \(\Delta KCE\) ta có:
\(BD=CE\left(gt\right),\widehat{HBD}=\widehat{KCE}\left(cmt\right)\Rightarrow\Delta HBD=\Delta KCE\) ( cạnh huyền - góc nhọn )
=> HB = CK ( 2 cạnh tương ứng ) ( ĐPCM )
b, Vì \(\Delta ABC\) cân tại A => AB = AC
Vì \(\widehat{ABC}=\widehat{ACB}\Rightarrow180^o-\widehat{ABC}=180^o-\widehat{ACB}\Rightarrow\widehat{ABH}=\widehat{ACK}\)
Xét \(\Delta AHB\) và \(\Delta AKC\) ta có:
\(AB=AC\left(cmt\right),\widehat{ABH}=\widehat{ACK}\left(cmt\right),HB=CK\left(cmt\right)\)\(\Rightarrow\Delta AHB=\Delta AKC\left(c.g.c\right)\)( ĐPCM )
c, Vì \(AB=AC,BD=CE\Rightarrow AB+BD=AC+CE\Rightarrow AD=CE\)
\(\Rightarrow\Delta ADE\) cân tại A \(\Rightarrow\widehat{ADE}=\widehat{AED}=\frac{180^o-\widehat{A}}{2}\left(1\right)\)
Vì \(\Delta ABC\) cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}=\frac{180^o-\widehat{A}}{2}\left(2\right)\)
Từ (1) và (2) => \(\widehat{ABC}=\widehat{ADE}\)
Mà \(\widehat{ABC}\) và \(\widehat{ADE}\) nằm ở bị trí đồng vị => HK song song với DE ( ĐPCM )
d, Vì \(\Delta HBD=\Delta KCE\Rightarrow DH=EK\) ( 2 cạnh tương ứng )
\(\widehat{BDH}=\widehat{CEK}\) ( 2 góc tương ứng ) \(\widehat{ADH}=\widehat{AEK}\)
Xét \(\Delta AHD\) và \(\Delta AKE\) ta có:
\(AD=AE\left(cmt\right),\widehat{AEK}=\widehat{ADH}\left(cmt\right),BD=CE\left(gt\right)\)
\(\Rightarrow\Delta AHD=\Delta AKE\left(c.g.c\right)\) ( ĐPCM )
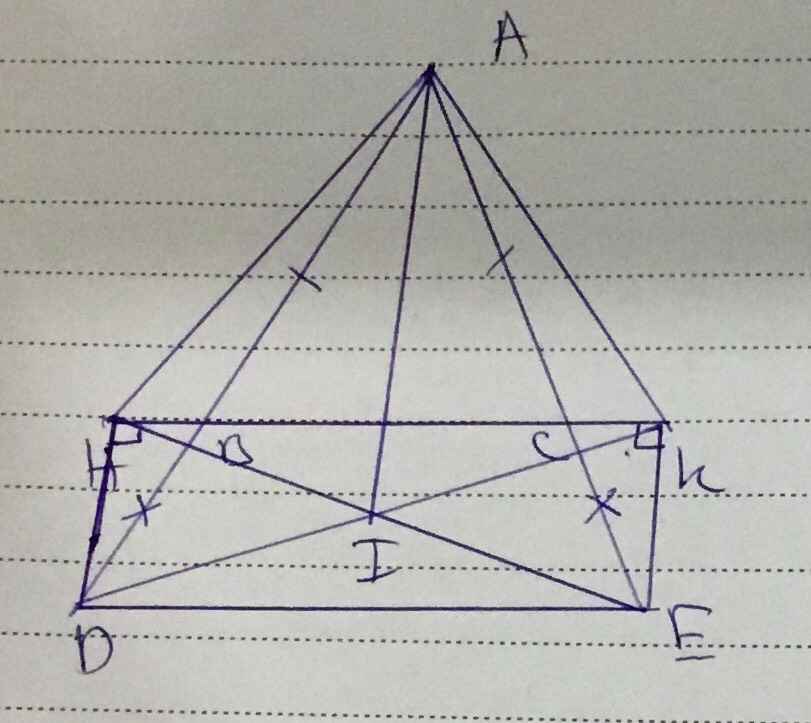
Xét tg ahd và tg ake
+có : ae+ec=ac
và ad+db=ab
mà :ad=ae ; bd=ce
=>AE=AD (1)
+có : góc AHD+ gócDHB=gócADH
và góc AKE+ góc EKC= góc AKC
=> gócAHD=gócAEK(2)
+ tg bdh=tg eck(vì : EC=BD; góc B= góc B và vuông tại D và D =90)
=>DB=EK (3)
Từ (1)(2) và (3) suy ra : tg AHD= tg AKEB(cgc)