Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 :
a, Xét tam giác BDA và tam giác KDC có:
Góc BDA= Góc KDC(đối đỉnh)
Góc B= Góc K(90 độ)
=>Tam giác BDA đồng dạng với tam giác KDC(g.g)
b,
Tam giác BDA đồng dạng với tam giác KDC ( cmt) => \(\frac{DB}{DA}=\frac{DK}{DC}\)
Xét tam giác DBK và tam giác DAC có:
Góc BDK= Góc DAC(đối đỉnh)
\(\frac{DB}{DA}=\frac{DK}{DC}\)
=>Tam giác DBK đồng dạng với tam giác DAC(c.g.c)
Bài 2 :
a) Xét tam giác ABH và tam giác AHD có:
\(\widehat{A}chung\)
\(\widehat{AHB}=\widehat{ADH}=90^o\)
⇒ tam giác ABH đồng dạng với tam giác AHD (g-g)
b)T/tự: tam giác AHC đồng dạng với tam giác AEH (g-g)
⇒ \(\widehat{ACH}=\widehat{AHE}\) ( 2 góc tương ứng)
Tam giác AEH đồng dạng với tam giác HEC
\(\widehat{ACH}=\widehat{AHE}\) (CM trên)
và \(\widehat{AEH}=\widehat{HEC}\) (= 900)
⇒\(\frac{AE}{HE}=\frac{EH}{EC}\)⇒\(AE\cdot EC=EH\cdot EH=EH^2\)
c) tam giác ADC đồng dạng với tam giác ABE (g-g) vì:
\(\widehat{A}\) chung
\(\widehat{ADC}=\widehat{AEB}=90^O\)
⇒ \(\widehat{ACD}=\widehat{ABE}\) ( 2 góc tương ứng)
Xét tam giác DBM và tam giác ECM có:
\(\widehat{ACD}=\widehat{ABE}\) (CM trên)
\(\widehat{DMB}=\widehat{EMC}\) (đối đỉnh)
⇒ tam giác DBM đồng dạng với tam giác ECM (g-g)
Bài 3 :

Bạn tự vẽ hình rồi đối chiếu kq nhé, có thể có sai sót đấy, ko chắc đúng hết đâu

Bài 2
gọi E là trung điểm của KB
Vì tam giác CKB có BM=MC ; BE=EK
=>EM//KC
Vì tam giác ENM có AN=AM ; KA//EM
=>EK=KN
Vì KN=KE=EB=>NK=1/2KB

a: BD/AD=BC/AC=5/4
b: Xét ΔHBA và ΔABC có
góc BHA=góc BAC
góc B chung
=>ΔHBA đồng dạng với ΔABC
c: Xét ΔDAC và ΔDKB có
góc DAC=góc DKB
góc ADC=góc KDB
=>ΔDAC đồng dạng với ΔDKB
=>DA/DK=DC/DB
=>DA*DB=DK*DC

a: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét ΔBAC có BD là phan giác
=>AD/AB=DC/BC
=>AD/3=DC/5=8/8=1
=>AD=3cm; DC=5cm
b: Xét ΔBAD vuông tại A va ΔBHI vuông tại H có
góc ABD=góc HBI
=>ΔBAD đồng dạng với ΔBHI
=>AD/HI=BA/BH
=>AD*BH=HI*BA
c: góc ADI=góc BIH=góc AID
=>ΔAID cân tại A

a: Xét tứ giác ADCE có
O là trung điểm chung của AC và DE
góc ADC=90 độ
Do đó: ADCE là hình chữ nhật
b: Xét tứ giác AEDB có
AE//DB
AE=DB
Do đó: AEDB là hình bình hành
c:BD=CD=BC/2=6cm
AO=OD=10/2=5cm
AD=8cm
P=(5+5+8)/2=18/2=9cm
\(S=\sqrt{9\cdot\left(9-8\right)\left(9-5\right)\left(9-5\right)}=\sqrt{9\cdot1\cdot4\cdot4}=3\cdot2\cdot2=12\left(cm^2\right)\)

a: Xét tứ giác ADCE có
O là trung điểm chung của AC và DE
góc ADC=90 độ
Do đó: ADCE là hình chữ nhật
b: Xét tứ giác AEDB có
AE//DB
AE=DB
Do đó: AEDB là hình bình hành
c:BD=CD=BC/2=6cm
AO=OD=10/2=5cm
AD=8cm
P=(5+5+8)/2=18/2=9cm
\(S=\sqrt{9\cdot\left(9-8\right)\left(9-5\right)\left(9-5\right)}=\sqrt{9\cdot1\cdot4\cdot4}=3\cdot2\cdot2=12\left(cm^2\right)\)

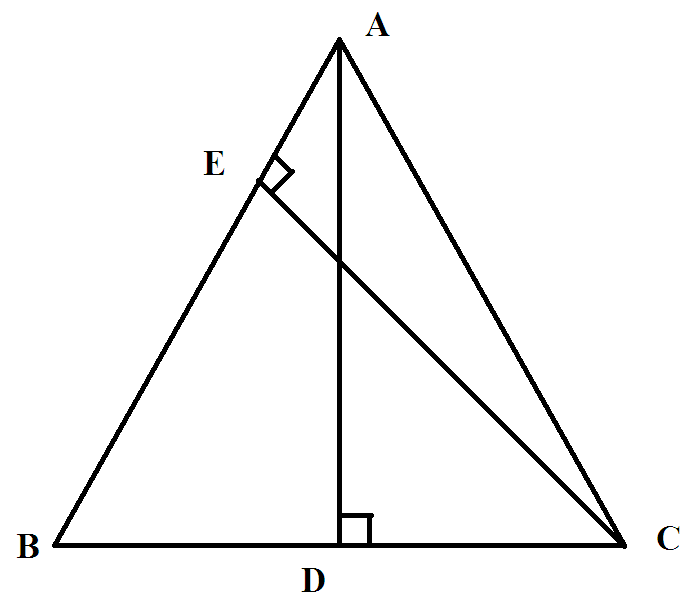
a) Xét △ABD và △CBE có:
\(\widehat{ADB}=\widehat{BEC}=90^o\)
\(\widehat{B}chung\)
Nên △ABD ∼ △CBE(g.g)
b)Theo câu a, ta có: △ABD ∼ △CB E
<=>\(\dfrac{AB}{BC}=\dfrac{BD}{BE}\Leftrightarrow AB.BE=BD.BC\)
c)Ta có:
\(BE=\dfrac{BD.BC}{AB}=\dfrac{3.12}{9}=4\left(cm\right)\)
b: Ta có: ΔABC cân tại A
mà AD là đường cao
nên Dlà trung điểm của BC
Xét ΔCDH vuông tại D và ΔADB vuông tại D có
góc HCD=góc BAD
Do đó; ΔCDH đồng dạng với ΔADB
Suy ra: CD/AD=DH/DB
hay \(AD\cdot DH=CD^2\)