Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

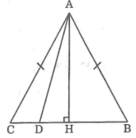
Kẻ AH ⊥ BC.
* Trường hợp H trùng với D
Ta có AH < AC (đường vuông góc ngắn hơn đường xiên)
Suy ra: AD < AC
* Trường hợp H không trùng với D
Giả sử D nằm giữa H và C.
Ta có: HD < HC
Suy ra: AD < AC (hình chiếu nhỏ hơn thì có đường xiên nhỏ hơn)
Vậy AD nhỏ hơn cạnh bên của tam giác cân ABC.

Kẻ \(AH\perp BC\)
- Nếu D trùng H thì \(AD< AC\) vì \(AH< AC\) ( đường vuông góc nhỏ hơn đường xiên )
- Nếu D không trùng H, giả sử D nằm giữa H và C. Ta có: \(HD< HC\)
\(\Rightarrow AD< AC\) ( hình chiếu nhỏ hơn thì đường xiên nhỏ hơn )
Vậy AD nhỏ hơn cạnh bên của \(\Delta ABC\)

Vì ΔBAC vuông tại B
nên AB<AC
góc ACB<90 độ
=>góc ACD>90 độ
=>AC<AD
góc ACD>90 độ
=>góc CDA<90 độ
=>góc ADE>90 độ
=>AD<AE
=>AB<AC<AD<AE

ABC cân A nên AD cũng là đường cao
\(BD=\dfrac{1}{2}BC=3\left(cm\right)\)
Áp dụng PTG: \(AD=\sqrt{AB^2-BD^2}=\sqrt{91}\left(cm\right)\)

a: AC=8cm
Xét ΔCBD có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔCBD cân tại C
hay CB=CD
Xét ΔCBD có
DK là đường trung tuyến
CA là đường trung tuyến
DK cắt CA tại M
Do đó: M là trọng tâm
=>AM=AC/2=8/3(cm)
b: Xét ΔCAD có
G là trung điểm của AC
GQ//AD
Do đó: Q là trung điểm của CD
Vì M là trọng tâm của ΔCDB nên B,M,Q thẳng hàng
