Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)\(\Delta ABH\) vuông tại H có:
BH2 =AB2 -AH2 =132 -122 =25( ĐL Pytago)
=> BH=5 cm
BC=BH+HC=5+16=21 cm
\(\Delta AHC\) vuông tại H có:
AH2 + HC2 =AC2 ( đl Pytago)
=> AC2 =122 + 162 =20 cm
b) \(\Delta AHB\) vuông tại H có: AB2 = AH2 +BH2 ( ĐL Pytago)
=> BH2 =AB2 - AH2 =132 - 122 =25
=> BH=5 cm
BC= BH+HC=5+16=21 cm
\(\Delta AHC\) vuông tại H có: AC2 = AH2 +HC2 ( đL Pytago)
=> AC2 = 122 + 162 =400
=> AC= 20 cm

a)
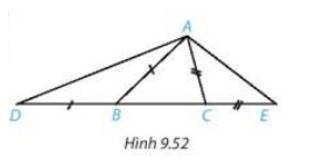
\(AB > AC \Rightarrow \widehat {ABC} < \widehat {ACB}\)( quan hệ giữa góc và cạnh đối diện trong tam giác ABC)
\(\begin{array}{l} \Rightarrow {180^0} - \widehat {ABD} < {180^0} - \widehat {ACE}\\ \Rightarrow \widehat {ABD} > \widehat {ACE}\end{array}\)
Vì BD= BA nên tam giác ABD cân tại B \( \Rightarrow \widehat {ABD} = {180^0} - 2\widehat {ADB}\)
Vì CE = CA nên tam giác ACE cân tại C \( \Rightarrow \widehat {ACE} = {180^0} - 2\widehat {AEC}\)
\(\begin{array}{*{20}{l}}{ \Rightarrow {{180}^0} - 2\widehat {ADB} > {{180}^0} - 2\widehat {AEC}}\\{ \Rightarrow \widehat {ADB} < \widehat {AEC}}\\{Hay{\mkern 1mu} \widehat {ADE} < \widehat {AED}}\end{array}\)
b) Xét tam giác ADE ta có : \(\widehat {ADB} < \widehat {AEC}\)
\( \Rightarrow AD > AE\)(Quan hệ giữa cạnh và góc đối diện trong tam giác).

A B C E D I
a) Xét tam giác ABD và EBD có:
BA = BE (gt)
\(\widehat{ABD}=\widehat{EBD}\) (Do BD là tia phân giác góc B)
BD chung
\(\Rightarrow\Delta ABD=\Delta EBD\left(c-g-c\right)\)
\(\Rightarrow AD=ED\) (Hai cạnh tương ứng)
b) Do \(\Delta ABD=\Delta EBD\left(cmt\right)\Rightarrow\widehat{BED}=\widehat{BAD}=90^o\)
Xét tam giác vuông ABC ta có \(\widehat{ABC}=90^o-\widehat{ACB}\)
Xét tam giác vuông DEC ta có \(\widehat{EDC}=90^o-\widehat{ACB}\)
Vậy nên \(\widehat{EDC}=\widehat{ABC}\)
c) Gọi giao điểm của AE và BD là I.
Xét tam giác ABI và tam giác EBI có:
AB = EB (gt)
\(\widehat{ABI}=\widehat{EBI}\)
BD chung
\(\Rightarrow\Delta ABI=\Delta EBI\left(c-g-c\right)\)
\(\Rightarrow\widehat{AIB}=\widehat{EIB}\) (Hai góc tương ứng)
Mà chúng lại ở vị trí kề bù nên \(\widehat{AIB}=\widehat{EIB}=90^o\)
Vậy nên \(AE\perp BD\)

a) tam giác ABC vuông tại A
=> AB2 + AC2 = BC2 (định lý py-ta-go)
=> 92 + AC2 = 152
=> AC2 = 225 - 81
=> AC2 = 144 => AC = \(\sqrt{144}=12cm\)
t i c k đúng nhé
a) trong tam giác ABC có: AB < AC < BC ( 9 < 12 < 15)
=> góc C < góc B < góc A (định lý)
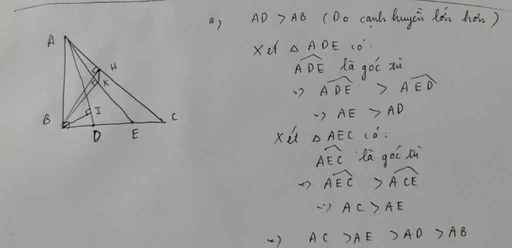

Vì ΔBAC vuông tại B
nên AB<AC
góc ACB<90 độ
=>góc ACD>90 độ
=>AC<AD
góc ACD>90 độ
=>góc CDA<90 độ
=>góc ADE>90 độ
=>AD<AE
=>AB<AC<AD<AE
vẽ hình hộ e với ạ