Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

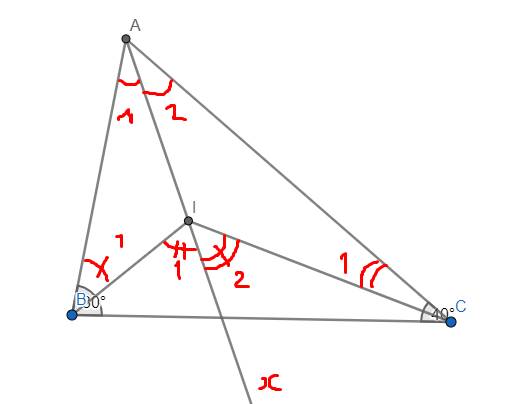
Ta có \(\widehat{I_1}=\widehat{A_1}+\widehat{B_1}\) và \(\widehat{I_2}=\widehat{A_2}+\widehat{C_1}\)
\(\Rightarrow\widehat{BIC}=\widehat{I_1}+\widehat{I_2}\)
\(=\left(\widehat{A_1}+\widehat{A_2}\right)+\left(\widehat{B_1}+\widehat{C_1}\right)\)
\(=\widehat{BAC}+\dfrac{\widehat{ABC}+\widehat{ACB}}{2}\)
\(=180^o-\left(\widehat{ABC}+\widehat{ACB}\right)+\dfrac{\widehat{ABC}+\widehat{ACB}}{2}\)
\(=180^o-\left(80^o+40^o\right)+\dfrac{80^o+40^o}{2}\)
\(=120^o\)
Vậy \(\widehat{BIC}=120^o\)
B1: Cho tam giác ABC có B=80, C=40 độ. Tia phân giác của góc B cắt AC tại D. Tính ADB.
B2: Cho ta giác ABC có B-C=20 độ. Đường phân giác AD của góc A cắt BC tại D. Tính ADB và ADC.
B3: Cho hình vẽ tính ACB

a) \(\widehat{IBC}=\frac{1}{2}\widehat{B}=\frac{1}{2}.80^0=40^0\)
\(\widehat{ICB}=\frac{1}{2}.\widehat{C}=\frac{1}{2}.40^0=20^0\)
\(\Rightarrow\widehat{BIC}=180^0-\widehat{IBC}-\widehat{ICB}=180^0-40^0-20^0=120^0\)
b) Ta có : \(\widehat{A}=80^0\)
\(\Rightarrow\widehat{B}+\widehat{C}=180^0-\widehat{A}=180^0-80^0=100^0\)
\(\Rightarrow\widehat{IBC}+\widehat{ICB}=\frac{\widehat{B}+\widehat{C}}{2}=\frac{100^0}{2}=50^0\)
\(\Rightarrow\widehat{BIC}=180^0-\left(\widehat{IBC}+\widehat{ICB}\right)=180^0-50^0=130^0\)

Ta có:góc ABI= góc IBC(BI là tia phân giác của góc ABC)
Góc AIB=IBC=80*÷2=40*
Lại có:ACI=ICB=40*÷2=20*(vì CI là tia phân giác của ACB)
Xét tam giác BIC có:IBC+ICB+BIC=180*(tổng 3 góc của tam giác)
=>BIC=180*-(IBC+ICB)=180*-(40*+20*)=180*-60*=120*