Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu a
Xét tam giác ABD và AMD có
AB = AM từ gt
Góc BAD = MAD vì AD phân giác BAM
AD chung
=> 2 tam guacs bằng nhau
Câu b
Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD
Bd = bm vì 2 tam giác ở câu a bằng nhau
Góc BDE bằng MDC đối đỉnh
=> 2 tam giác bằng nhau

4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
c: AE=AF
ME=MF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng

e) vì AC vuông góc vs BK , KE ( kéo dài ED)vuông góc với BC mà AC và KE cắt nhau tại D => D là trực tâm của tam giác KBC => BD vuoogn góc với KC ( 1 ) .M là trung điểm của KC => BM là đường cao đồng thời là đường trung trực của tam giác KBC ( 2 ) . từ ( 1 ) và ( 2 ) => B, D , M thằng hàng

Diễn giải:
- Khi cộng, trừ số thập phân ta tiến hành cộng hoặc trừ các phần tương ứng của các số đó.
Ví dụ 1:
Tính 0,25 + 2,5 ta làm như sau: 5 + 0 = 5 , 2 + 5 =7, 0 + 2 = 2. Vậy 0,25 + 2,5 = 2.75
Tính 8,6 - 2,7 ta làm như sau: 6 - 7 không trừ được ta lấy 16 - 7 = 9, tiếp tục 8 - 2 trừ thêm 1 nữa tức là 8 -3 = 5. Vậy 8,6 - 2,7 = 5,9
- Với phép nhân, chia các số thập phân ta cần viết chúng dưới dạng phân số.

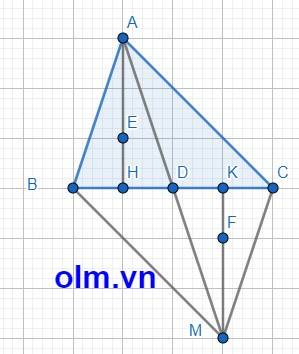
Xét tam giác ACD và tam giác MBD có:
AD = DM (gt)
BD = DC (gt)
\(\widehat{BDM}\) = \(\widehat{ADC}\) (hai góc đối đỉnh)
⇒ \(\Delta\)ACD = \(\Delta\) MBD (c-g-c)
Xét tứ giác ABMC có
AD = DM
BD = DC
⇒ tứ giác ABMC là hình bình hành vì tứ giác có hai đường chéo căt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành.
⇒ AC // BM
⇒ \(\widehat{ABM}\) = \(\widehat{MCA}\) (vì tứ giác ABMC là hình bình hành)
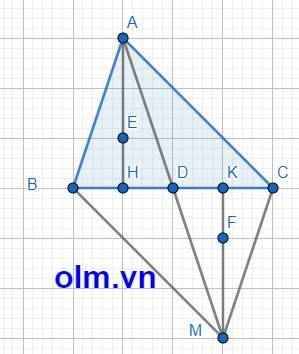
xét tam giác ACD và tam giác MBD có
AD=DM [ gt ]
BD=DC[ gt ]
BDM = ADC hai góc đối đỉnh
suy ra tam giác ACD= tam giác MBD [ c-g-c]
xét tứ giác ABMC có
AD = DM
BD=DC
suy ra tứ giác ABMC là hình bình hành vì tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành
suy ra ABM=MCA vì tứ giác ABMC là hình bình hành .
a, Xét ∆ABM và ∆ECM, ta có:
- AM = ME (gt)
- \(\widehat{AMB}=\widehat{EMC}\) (đối đỉnh)
- MB = MC (M là trung điểm BC)
=> ∆ABM = ∆ECM (c-g-c)
b, Xét ∆AMC và ∆BME, ta có:
- AM = ME (gt)
- \(\widehat{AMC}=\widehat{BME}\) (đối đỉnh)
- MB = MC (M là trung điểm BC)
=> ∆AMC = ∆BME (c-g-c)
=> AC = BE
c, Xét ∆AHB và ∆DHB, ta có:
- AH = HD (gt)
- \(\widehat{AHB}=\widehat{DHB}=90^o\)
- BH là cạnh chung (gt)
=> ∆AHB = ∆DHB (c-g-c)
=> \(\widehat{ABH}=\widehat{DBH}\)
=> BM là phân giác góc ABM
d,