


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a: Xét tứ giác AMDN có góc AMD=góc AND=góc MAN=90 độ
nên AMDN là hình chữ nhật
Suy ra: AD=MN
b: Xét tứ giác AMHD có góc AMD=góc AHD=90 độ
nên AMHD là tứ giác nội tiếp
=>A,M,H,D cùng thuộc 1 đường tròn (1)
Xét tứ giác AMDN có góc AMD+góc AND=180 độ
nên AMDN là tứ giác nội tiếp
=>A,M,D,N cùng thuộc 1 đường tròn(2)
Từ (1) và (2) suy ra A,M,H,D,N cùg thuộc 1 đường tròn
=>AMHN là tứ giác nội tiếp
=>góc AHM=90 độ

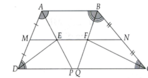
a) Gọi P và Q lần lượt là giao điểm của AE, AF với CD.
Chứng minh tương tự 2B.
b) Ta có:
M N = 1 2 ( A B + C D ) = 1 2 ( a + c )
Lại có:
c = CD = CQ + QD = BC + QD = b + QD (do tam giác BCQ cân) Þ QD = c - b.
Trong hình thang ABQD có M là trung điểm của AD và MF//DQ nên chứng minh được F là trung điểm của BQ, từ đó chứng minh MF là đường trung bình của hình thang ABQD.
Vì MF là đường trung bình của hình thang ABQD.
Þ M F = 1 2 ( A B + D Q ) = 1 2 ( a + c − b )
Mặt khác, FN là đường trung bình của tam giác BCQ, tức là F N = 1 2 C Q = 1 2 b .

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét tứ giác AMDN có \(\widehat{AMD}=\widehat{AND}=\widehat{MAN}=90^0\)
nên AMDN là hình chữ nhật
c: AMDN là hình chữ nhật
=>AD cắt MN tại trung điểm của mỗi đường
mà I là trung điểm của AD
nên I là trung điểm của MN
=>M,I,N thẳng hàng
d: Ta có: ΔABC vuông tại A
mà AD là đường trung tuyến
nên \(AD=\dfrac{BC}{2}=\dfrac{10}{2}=5\left(cm\right)\)