Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Δ=(-4)^2-4(m^2+3m)
=16-4m^2-12m
=-4(m^2+3m-4)
=-4(m+4)(m-1)
Để phươg trình có hai nghiệm thì Δ>=0
=>-4(m+4)(m-1)>=0
=>(m+4)(m-1)<=0
=>-4<=m<=1
x1^2+x2^2=6
=>(x1+x2)^2-2x1x2=6
=>4^2-2(m^2+3m)=6
=>16-2m^2-6m-6=0
=>-2m^2-6m+10=0
=>m^2+3m-5=0
=>\(m=\dfrac{-3\pm\sqrt{29}}{2}\)
\(\Delta'=4-m^2-3m\ge0\Rightarrow-4\le m\le1\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=4\\x_1x_2=m^2+3m\end{matrix}\right.\)
\(x_1^2+x_2^2=6\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=6\)
\(\Leftrightarrow4^2-2\left(m^2+3m\right)=6\)
\(\Leftrightarrow m^2+3m-5=0\Rightarrow\left[{}\begin{matrix}m=\dfrac{-3+\sqrt{29}}{2}>1\left(loại\right)\\m=\dfrac{-3-\sqrt{29}}{2}< -4\left(loại\right)\end{matrix}\right.\)
Vậy ko tồn tại m thỏa mãn yêu cầu đề bài

\(\Delta=9-4\left(-m^2+m+2\right)=4m^2-4m+1=\left(2m-1\right)^2\)
Pt có 2 nghiệm pb khi \(m\ne\dfrac{1}{2}\)
Do vai trò của 2 nghiệm là như nhau, giả sử: \(\left\{{}\begin{matrix}x_1=\dfrac{3-\left(2m-1\right)}{2}=2-m\\x_2=\dfrac{3+2m-1}{2}=m+1\end{matrix}\right.\)
\(x_1^2+x_2^2=5\Leftrightarrow\left(2-m\right)^2+\left(m+1\right)^2=5\)
\(\Leftrightarrow m^2-m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=1\end{matrix}\right.\)

Phương trình có hai nghiệm phân biệt x1, x2 ⇔ ∆ = 52 – 4(3m + 1) > 0 ⇔ 21 – 12m > 0
ó m < 21/12
Với m < 21/12 , ta có hệ thức x 1 + x 2 = 5 x 1 x 2 = 3 m + 1 V i e t '
⇒ | x 1 − x 2 | = ( x 1 − x 2 ) 2 = ( x 1 + x 2 ) 2 − 4 x 1 x 2 = 5 2 − 4 ( 3 m + 1 ) = 21 − 12 m = > | x 1 2 − x 2 2 | = | ( x 1 + x 2 ) ( x 1 − x 2 ) | = | 5 ( x 1 − x 2 ) | = 5 | x 1 − x 2 | = 5 21 − 12 m
Ta có: | x 1 2 − x 2 2 | = 15 ⇔ 5 21 − 12 m = 15 ⇔ 21 − 12 m = 3 ⇔ 21 − 12 m = 9 ⇔ 12 m = 12 ⇔ m = 1 (t/m)
Vậy m = 1 là giá trị cần tìm

Sửa lại đề:
x2 - (3m - 1)x + 2m2 - m = 0
Ta có: \(\Delta\) = [-(3m - 1)]2 - 4.1.(2m2 - m) = 9m2 - 6m + 1 - 8m2 + 4m = m2 - 2m + 1 = (m - 1)2 \(\ge\) 0
\(\Rightarrow\) x1 = \(\dfrac{3m-1+m-1}{2}=\dfrac{4m-2}{2}=2m-1\)
x2 = \(\dfrac{3m-1-m+1}{2}=\dfrac{2m}{2}=m\)
Ta có: x1 = x22 \(\Leftrightarrow\) 2m - 1 = m2 \(\Leftrightarrow\) m2 - 2m + 1 = 0 \(\Leftrightarrow\) (m - 1)2 = 0
\(\Leftrightarrow\) m - 1 = 0 \(\Leftrightarrow\) m = 1
Vậy m = 1
Chúc bn học tốt!

a,để pt có nghiệm kép
\(\Delta=m^2-\left(m^2-m+1\right)=m-1=0\Leftrightarrow m=1\)
\(x_1=x_2=\dfrac{2m}{2}=m=1\)
b, để pt có nghiệm \(m\ge1\)
c, Ta có \(\left(x_1+x_2\right)^2-4x_1x_2=6\)
Thay vào ta đc \(4m^2-4\left(m^2-m+1\right)=6\)
\(\Leftrightarrow4m=10\Leftrightarrow m=\dfrac{5}{2}\left(tm\right)\)

Bài 1:
a, Thay m=-1 vào (1) ta có:
\(x^2-2\left(-1+1\right)x+\left(-1\right)^2+7=0\\
\Leftrightarrow x^2+1+7=0\\
\Leftrightarrow x^2+8=0\left(vô.lí\right)\)
Thay m=3 vào (1) ta có:
\(x^2-2\left(3+1\right)x+3^2+7=0\\ \Leftrightarrow x^2-2.4x+9+7=0\\ \Leftrightarrow x^2-8x+16=0\\ \Leftrightarrow\left(x-4\right)^2=0\\ \Leftrightarrow x-4=0\\ \Leftrightarrow x=4\)
b, Thay x=4 vào (1) ta có:
\(4^2-2\left(m+1\right).4+m^2+7=0\\ \Leftrightarrow16-8\left(m+1\right)+m^2+7=0\\ \Leftrightarrow m^2+23-8m-8=0\\ \Leftrightarrow m^2-8m+15=0\\ \Leftrightarrow\left(m^2-3m\right)-\left(5m-15\right)=0\\ \Leftrightarrow m\left(m-3\right)-5\left(m-3\right)=0\\ \Leftrightarrow\left(m-3\right)\left(m-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=3\\m=5\end{matrix}\right.\)
c, \(\Delta'=\left[-\left(m+1\right)\right]^2-\left(m^2+7\right)=m^2+2m+1-m^2-7=2m-6\)
Để pt có 2 nghiệm thì \(\Delta'\ge0\Leftrightarrow2m-6\ge0\Leftrightarrow m\ge3\)
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1x_2=m^2+7\end{matrix}\right.\)
\(x_1^2+x_2^2=0\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=0\\ \Leftrightarrow\left(2m+2\right)^2-2\left(m^2+7\right)=0\\ \Leftrightarrow4m^2+8m+4-2m^2-14=0\\ \Leftrightarrow2m^2+8m-10=0\\ \Leftrightarrow\left[{}\begin{matrix}m=1\left(ktm\right)\\m=-5\left(ktm\right)\end{matrix}\right.\)
\(x_1-x_2=0\\ \Leftrightarrow\left(x_1-x_2\right)^2=0\\ \Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=0\\ \Leftrightarrow\left(2m+2\right)^2-4\left(m^2+7\right)=0\\ \Leftrightarrow4m^2+8m+4-4m^2-28=0\\ \Leftrightarrow8m=28=0\\ \Leftrightarrow m=\dfrac{7}{2}\left(tm\right)\)
Bài 2:
a,Thay m=-2 vào (1) ta có:
\(x^2-2x-\left(-2\right)^2-4=0\\ \Leftrightarrow x^2-2x-4-4=0\\ \Leftrightarrow x^2-2x-8=0\\ \Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)
b, \(\Delta'=\left(-m\right)^2-\left(-m^2-4\right)\ge0=m^2+m^2+4=2m^2+4>0\)
Suy ra pt luôn có 2 nghiệm phân biệt
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-m^2-4\end{matrix}\right.\)
\(x_1^2+x_2^2=20\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=20\\ \Leftrightarrow2^2-2\left(-m^2-4\right)=20\\ \Leftrightarrow4+2m^2+8-20=0\\ \Leftrightarrow2m^2-8=0\\ \Leftrightarrow m=\pm2\)
\(x_1^3+x_2^3=56\\ \Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=56\\ \Leftrightarrow2^3-3\left(-m^2-4\right).2=56\\ \Leftrightarrow8-6\left(-m^2-4\right)-56\\ =0\\ \Leftrightarrow8+6m^2+24-56=0\\ \Leftrightarrow6m^2-24=0\\ \Leftrightarrow m=\pm2\)
\(x_1-x_2=10\\ \Leftrightarrow\left(x_1-x_2\right)^2=100\\ \Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2-100=0\\ \Leftrightarrow2^2-4\left(-m^2-4\right)-100=0\\ \Leftrightarrow4+4m^2+16-100=0\\ \Leftrightarrow4m^2-80=0\\ \Leftrightarrow m=\pm2\sqrt{5}\)

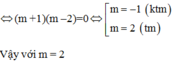
Để PT có hai nghiệm x1,x2 thì:
Δ' = (-1)2 - 1.(3m-2) > 0
<=> m <1
Áp dụng Viet, ta có :
x1 + x2 = -2
x1.x2 = 3m-2
Ta có :
x12 + x22 = (x1 + x2)2 - 2x1.x2 = (-2)2 - 2(3m-2) = 20
<=> 4 -6m + 4 = 20
<=> m = -2 (thỏa mãn)
Vậy m = -2