Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\dfrac{m-3}{x-4}=m^2-m-6\)
=>\(\dfrac{m-3}{x-4}-\left(m-3\right)\left(m+2\right)=0\)
=>\(\left(m-3\right)\left(\dfrac{1}{x-4}-m-2\right)=0\)
=>\(\dfrac{1}{x-4}-m-2=0\)
=>\(\dfrac{1}{x-4}=m+2\)
=>\(\left(m+2\right)\left(x-4\right)=1\)
=>\(x\left(m+2\right)-4m-8-1=0\)
=>\(x\left(m+2\right)=4m+9\)
Để phương trình có nghiệm duy nhất thì \(m+2\ne0\)
=>\(m\ne-2\)
mà \(m\ne3\)
nên \(m\notin\left\{-2;3\right\}\)
Để phương trình vô nghiệm thì m+2=0
=>m=-2
;
a) Phương trình tham số của d là:
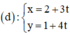
b) d nhận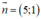 
là 1 vec tơ pháp tuyến
⇒ d nhận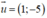 
là 1 vec tơ chỉ phương
Phương trình tham số của đường thẳng d là:
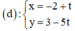
a, ĐK: \(x\le-1,x\ge3\)
\(pt\Leftrightarrow2\left(x^2-2x-3\right)+\sqrt{x^2-2x-3}-3=0\)
\(\Leftrightarrow\left(2\sqrt{x^2-2x-3}+3\right).\left(\sqrt{x^2-2x-3}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^2-2x-3}=-\dfrac{3}{2}\left(l\right)\\\sqrt{x^2-2x-3}=1\end{matrix}\right.\)
\(\Leftrightarrow x^2-2x-3=1\)
\(\Leftrightarrow x^2-2x-4=0\)
\(\Leftrightarrow x=1\pm\sqrt{5}\left(tm\right)\)
b, ĐK: \(-2\le x\le2\)
Đặt \(\sqrt{2+x}-2\sqrt{2-x}=t\Rightarrow t^2=10-3x-4\sqrt{4-x^2}\)
Khi đó phương trình tương đương:
\(3t-t^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=0\\t=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2+x}-2\sqrt{2-x}=0\\\sqrt{2+x}-2\sqrt{2-x}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2+x=8-4x\\2+x=17-4x+12\sqrt{2-x}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{6}{5}\left(tm\right)\\5x-15=12\sqrt{2-x}\left(1\right)\end{matrix}\right.\)
Vì \(-2\le x\le2\Rightarrow5x-15< 0\Rightarrow\left(1\right)\) vô nghiệm
Vậy phương trình đã cho có nghiệm \(x=\dfrac{6}{5}\)
1,
a, với m=1 , phương trình có nghiệm x=\(\frac{1}{2}\)
với m\(\ne1\) , \(_{\Delta}\)=m
- nếu m< 0 : pt vô nghiệm
-nếu m=0: pt có 1 nghiệm kép x=1
-nếu m>0( và m\(\ne\)1) : pt có 2 nghiệm
\(x_1=\frac{-1-\sqrt{m}}{m-1}\) và \(x_2=\frac{-1+\sqrt{m}}{m-1}\)
b, pt có 2 nghiệm trái dấu nếu
m-1\(\ne\)0 và \(\frac{-1}{m-1}\)<0 \(\Leftrightarrow\)m>1
c, \(m\ne1\) và m>0, pt có 2 nghiệm x1 và x2
1=x12 +x22=(x1+x2)2-2x1x2=\(\left(\frac{2}{m-1}\right)^2+\frac{2}{m-1}\Rightarrow m=2+\sqrt{5}\)
2,
giả sử 2 pt đều có nghiệm thì phải có:
\(\Delta_1=1-4a\ge0\) và \(\Delta_2=a^2-4\ge0\Leftrightarrow a\le-2\)
giả sử k là 1 nghiệm chung thì ta phải có:
k2+k+a=k2+ka+1
\(\Rightarrow\) k(a-1)=a-1 \(\Rightarrow\)k=1 (vì \(a\le-2\) nên a-1\(\ne\)0)
thay k=1 vào 1 pt ta tính được a=-2
thử lại: a=-2 vào các pt ta thấy dúng là 2 pt có nghiệm chung là x=1
a) Phương trình đường thẳng Δ đi qua M(–5; –8) và có hệ số góc k = –3 là:
y = –3.(x + 5) – 8 ⇔ 3x + y + 23 = 0.
b) Ta có: A(2; 1), B(–4; 5) ⇒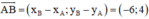 
Δ đi qua hai điểm A(2; 1) và B(–4; 5)
⇒ Δ nhận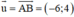 
là một vtcp
⇒ Δ nhận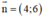 
là một vtpt.
Phương trình tổng quát của đường thẳng Δ là:
(Δ) : 4(x – 2) + 6(y -1) = 0
Hay 4x + 6y – 14 = 0 ⇔ 2x + 3y – 7 = 0.
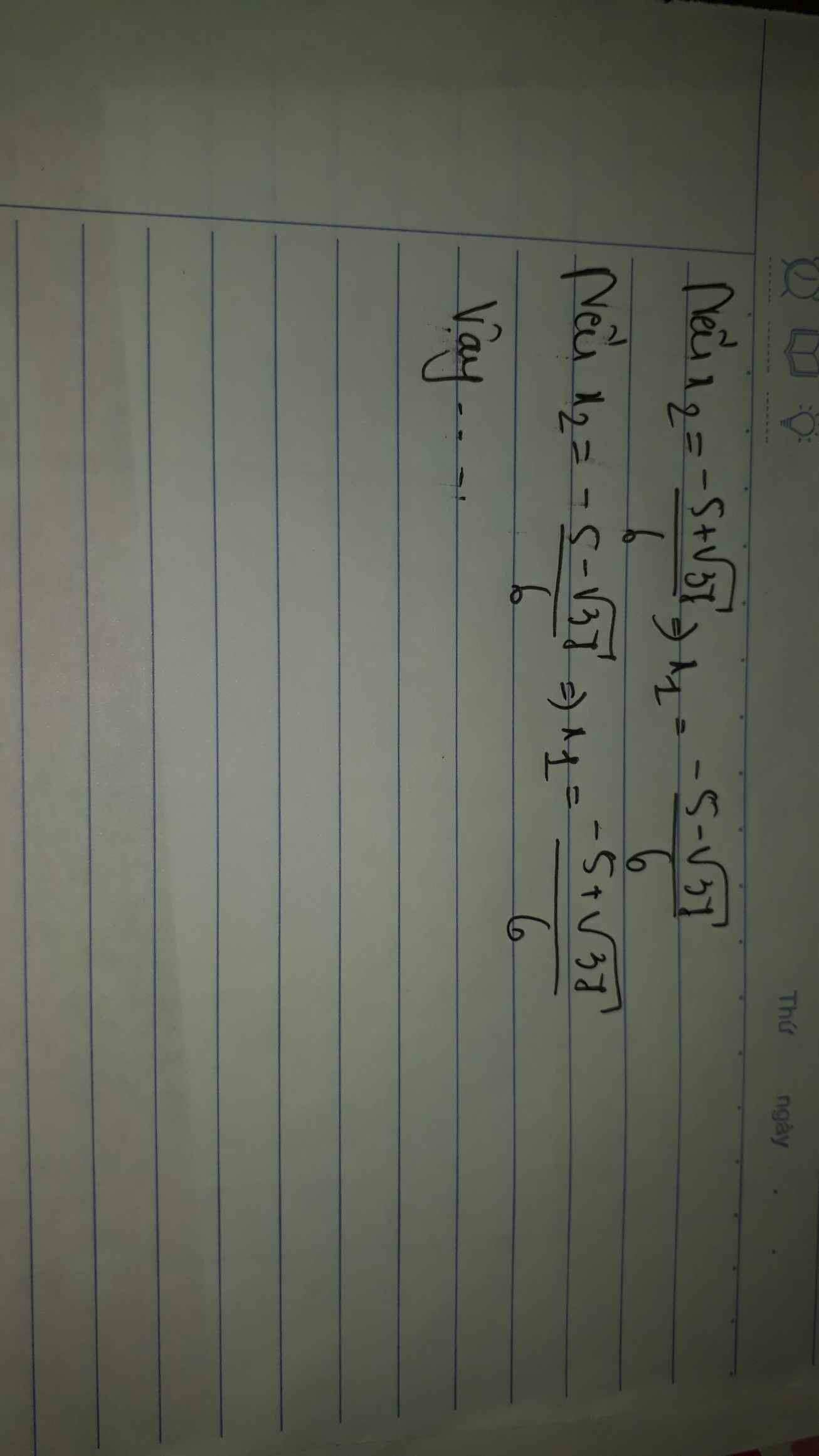
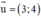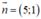
+) Thay \(m=2\) vào phương trình \(\left(m^2-4\right)x+2=m\) ta được:
\(\left(2^2-4\right)x+2=2\)
\(\Leftrightarrow0x+2=2\)
\(\Leftrightarrow0x=0\)
Vậy pt vô nghiệm
+) Thay \(m=-2\) vào phương trình \(\left(m^2-4\right)x+2=m\) ta được:
\(\left[\left(-2\right)^2-4\right]x+2=-2\)
\(\Leftrightarrow0x+2=-2\)
\(\Leftrightarrow0x=-4\)
Vậy pt vô nghiệm
+) Thay \(m=-2,2\) vào phương trình \(\left(m^2-4\right)x+2=m\) ta được:
\(\left[\left(-2,2\right)^2-4\right]x+2=2,2\)
\(\Leftrightarrow0,84x=-4,2\)
\(\Leftrightarrow x=-5\)
Vậy pt có nghiệm \(x=-5\)
Bạn xem lại đề hộ mình là \(\left(m2-4\right)x+2=m\) hay \(\left(m^2-4\right)x+2=m\) vậy bạn