
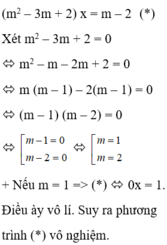

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

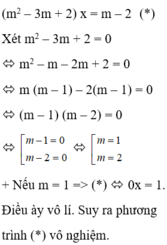


a) ý bạn là x=2 à
Với x=2
pt <=>\(2m^2-2=m^2+3m+8\Leftrightarrow m^2-3m-10=0\Leftrightarrow\left(m-5m\right)+\left(2m-10\right)=0\)
\(\Leftrightarrow\left(m+2\right)\left(m-5\right)=0\Leftrightarrow\orbr{\begin{cases}m+2=0\\m-5=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}m=-2\\m=5\end{cases}}\)
Vậy \(m\in\left\{5;-2\right\}\)thì pt có nghiệm x=2
b)c) pt<=>\(m^2x-4x=m^2+3m+2\Leftrightarrow x\left(m^2-4\right)=\left(m^2+2m\right)+\left(m+2\right)\)
\(\Leftrightarrow x\left(m-2\right)\left(m+2\right)=\left(m+2\right)\left(m+1\right)\)
Với \(m\ne-2\)pt <=> 0x=0 <=> pt có vô số nghiệm
Với \(m\ne2\)pt <=> 0x=12 <=> pt vô nghiệm
Với \(m\ne\pm2\)pt có nghiệm duy nhất \(x=\frac{m+1}{m-2}\)

a: Khi m=3 thì pt sẽ là 0x+0=0(luôn đúng)
b: Để phương trình có nghiệm duy nhất thì m-3<>0
hay m<>3
Để phương trình có vô số nghiệm thì m-3=0
hay m=3

ĐK: \(\hept{\begin{cases}x\ne2\\x\ne-m-1\end{cases}}\)
\(\frac{x+2}{x-2}+\frac{m-x}{x+m+1}=0\)(1)
=> ( x + 2 ) ( x + m + 1 ) + ( m - x ) ( x - 2 ) = 0
<=> (m + 3 ) x + 2 ( m + 1 ) + ( m + 2 ) x - 2m = 0
< => ( 2m + 5 ) x + 2 = 0 (2)
TH1: 2m + 5 = 0 <=> m = -5/2
Khi đó (2) trở thành: 0x + 2 = 0 => phương trình vô nghiệm với mọi x
=> m = -5/2 thỏa mãn
TH2: 2m + 5 \(\ne\)0 <=> m \(\ne\)-5/2
khi đó: (2) có nghiệm: \(x=-\frac{2}{2m+5}\)
( 1) vô nghiệm <=> (2) có nghiệm x = 2 hoặc x = -m -1
<=> \(\orbr{\begin{cases}-\frac{2}{2m+5}=-m-1\\-\frac{2}{2m+5}=2\end{cases}}\)
Giải: \(-\frac{2}{2m+5}=-m-1\)
<=> 2 = ( m + 1 ) ( 2m + 5 )
<=> 2m^2 +7m +3= 0
<=> m = -1/2 hoặc m = -3 (tm m khác -5/2)
Giải: \(-\frac{2}{2m+5}=2\)
<=> 2m + 5 = - 1 <=> m = - 3 (tm)
Vậy m = -5/2; m = -3; m = -1/2 thì phương trình vô nghiệm.

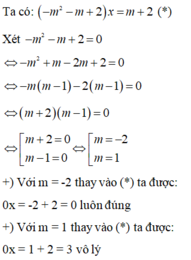
Vậy với m = -2 thì phương trình đã cho có vô số nghiệm.
Đáp án cần chọn là: C

a,để PT trở thành bậc nhất một ản thì m-3\(\ne0\Leftrightarrow m\ne3\)
thay x=2 vào biểu thức ta có m=-143(tm)