Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi phân số đó là \(\frac{a}{7}\)
Ta có : \(\frac{a}{7}=\frac{a+16}{7\times5}=\frac{a+16}{35}\)
=> \(\frac{a}{7}=\frac{a+16}{35}\)
=> \(\frac{a\times5}{35}=\frac{a+16}{35}\)
=> a x 5 = a + 16
=> a x 5 - a = 16
=> a x 4 = 16
=> a = 16 : 4
=> a = 4
Vậy phân số đó là \(\frac{4}{7}\)
Gọi phân số đó là \(\frac{a}{7}\)
Ta có: \(\frac{a+16}{7\times5}=\frac{a+16}{35}\)
\(\Rightarrow\) \(\frac{a}{7}=\frac{a+16}{35}\)
\(\Rightarrow\) a + 16 = a x 5
\(\Rightarrow\) 16 = a x 5 - a
\(\Rightarrow\) 16 = a x 4
\(\Rightarrow\) a = 16 : 4
\(\Rightarrow\) a = 4
Vậy, phân số đó là \(\frac{4}{7}\).

Đáp án C
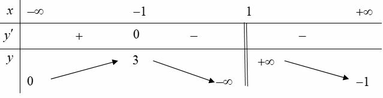
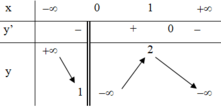
Dựa vào bảng biến thiên của đồ thị hàm số ⇒ f ( x ) = 3 m có 3 nghiệm phân biệt khi và chỉ khi 3 m ≤ − 3 ⇔ m ≤ − 1

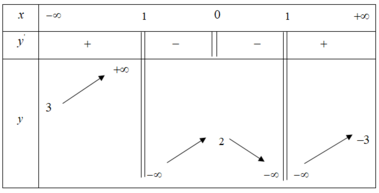
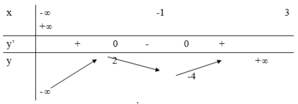
Phương trình tương đương với: f ( x ) = - m 2 phương trình có 3 nghiệm thực phân biệt - 4 < - m 2 < 2 ⇔ - 4 < m < 8 Các giá trị nguyên dương là m ∈ 1 , 2 . . . 7
Chọn đáp án B.

gọi mẫu số là b suy ra tử là (b+50). theo bài có:(b+57)=3x(b+7). giải ra b=18
gọi mẫu số là b suy ra tử là (b+50). theo bài có:(b+57)=3x(b+7). giải ra b=18

Đáp án D
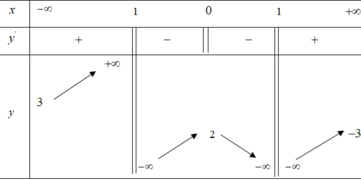
Từ bảng biến thiên ta thấy với m = 2 hoặc m ≤ 1 thì đồ thị hàm số y = f(x) cắt đường thẳng y = m tại 2 điểm phân biệt hay phương trình f(x) = m có 2 nghiệm phân biệt.



Gỉai
a) Theo đề bài, ta có :
x + y + 12
Vậy, số tự nhiên y là :
( 72 - 12 ) = 30
Và số tự nhiên x là
x - y = 12
30 + 12 = 42
=> Phân số \(\frac{x}{y}\) = \(\frac{7}{5}\)
b) Có 2 cách giải là :
- Cách 1 :
Gọi số cần tiền là n. Theo đề bài, ta có :
\(\frac{x}{y}\) = \(\frac{42-7}{30-n}\) = \(\frac{7}{5}\) => 35 . 5 = 210 - 7n
=> 175 = 210 - 7n
=> n = ( 210 - 175 ) : 7
=> n = 5
- Cách 2 :
\(\frac{x}{y}\) =\(\frac{42-7}{30-n}\) = \(\frac{7}{5}\) => \(\frac{35}{30-n}\) = \(\frac{7}{5}\)
=> 30 - n = 25
=> n = 30 - 25
=> n = 5