Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Số nghịch đảo của \(\frac{a}{b}\) là \(\frac{b}{a}\)
b) \(-\frac{17}{7}.x=\frac{7}{-17}\Leftrightarrow x=\frac{7}{-17}:-\frac{17}{7}=\frac{49}{289}\)

Lời giải:
Ta có các điều sau:
\(\left\{\begin{matrix} a+b\equiv 0\pmod k\\ c+d\equiv 0\pmod k\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a\equiv -b\pmod k\\ d\equiv-c\pmod k\end{matrix}\right.\)
Áp dụng tính chất nhân của mo- đun:
\(\Rightarrow ad\equiv (-b)(-d)=bd\pmod k\) . Suy ra $ad-bc$ chia hết cho $k$
Do đó ta có đpcm

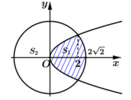
Diện tích hình tròn S = 8 π
Phương trình hoành độ giao điểm của (P) và (C) là
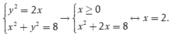
Suy ra 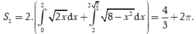
Suy ra
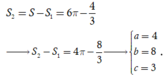
Chọn C.

- Tỉ số của :
-0,75 và 1,25 là -0,75 : 1,25 = -0,75/1,25
-2/1/3 và -3,15 là -2/1/3 :-3,15
-4/3/4 và 7/3 là -4/3/4 : 7/3
- - năm tỉ số là 1/2 , 2/3 , 3/4 , 4/5 , 5/6
- - giống : đều được viết dưới dạng a/b
- -Khác : Khi nói đến tỉ số a/b thì a và b có thể là các số nguyên,phân số,hỗn số,...Còn khi nói phân số a/b thì cả a và b đều là các số nguyên

Giả sử z 1 ; z 2 là các nghiệm của phương trình a z 2 + bz + c = 0 với z 1 = 1
Theo định lí Viet ta có:
z 1 z 2 = c a ⇔ z 2 = c a 1 z 1 ⇒ z 2 = c a . 1 z 1 = 1
Bởi vì
z 1 + z 2 = - b a a = b ⇒ z 1 + z 2 2 = 1
Suy ra
z 1 + z 2 z 1 + z 2 1 ⇔ z 1 + z 2 1 z 1 + 1 z 2 = 1 ⇔ z 1 + z 2 2 = z 1 z 2 ⇔ b 2 = a c
Đáp án B

a: Ta có: \(2x^3-5x^2+8x-3=0\)
\(\Leftrightarrow2x^3-x^2-4x^2+2x+6x-3=0\)
=>2x-1=0
hay x=1/2

ta có: \(\frac{a}{b}:\frac{c}{d}=\frac{a}{b}.\frac{c}{d}\Leftrightarrow\frac{a}{b}.\frac{d}{c}=\frac{a}{b}.\frac{c}{d}\Leftrightarrow\frac{a.d}{b.c}=\frac{a.c}{bd}\Leftrightarrow\frac{d}{c}=\frac{c}{d}\Leftrightarrow d^2=c^2\)
suy ra d=c hoặc d=-c
suy ra \(\frac{c}{d}=\frac{c}{c}=1\) hoặc \(\frac{c}{d}=\frac{c}{-c}=-1\)
Thay b + c = a vào ta có :
\(\frac{a}{b}.\frac{a}{c}=\frac{b+c}{b}.\frac{b+c}{c}=\frac{\left(b+c\right)^2}{bc}\) (1)
và \(\frac{a}{b}+\frac{a}{c}=\frac{ac+ab}{bc}=\frac{a.\left(b+c\right)}{bc}=\frac{\left(b+c\right).\left(b+c\right)}{bc}=\frac{\left(b+c\right)^2}{bc}\) (2)
Từ (1) và (2) suy ra \(\frac{a}{b}.\frac{a}{c}=\frac{a}{b}+\frac{a}{c}\)
Có : b+c=a
Thay vào , ta được:
a/b=a/c=> b+c/b.b+c/c=(b+c)2/bc và a/b+a/c=ac+ad/bc=a(b+c)/bc=(bc+c)(b+c)/bc=(b+c)2/bc
Từ trên ta có thể suy ra rằng :
a/b.a/c=a/b+a/c