Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
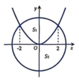
Phương trình đường tròn tâm O có bán kính R = 2 2 là x 2 + y 2 = 8 .
Ta có parabol và đường tròn như hình vẽ bên.
Giao điểm của parabol và đường tròn là nghiệm của hệ phương trình
x 2 + y 2 = 8 y = x 2 2 ⇔ x = ± 2 y = 2
Vì parabol và đường tròn đều đối xứng qua trục Oy nên ta có
S = 2 ∫ 0 2 8 - x 2 - x 2 2 d x .
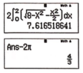
Bấm máy tính, ta được kết quả như hình bên. Ta biết S = a π + b c nên ta thao tác tiếp theo trên máy như hình bên.
Vậy ta có S = 2 π + 4 3 . Do đó ta có a = 2 , b = 4 , c = 3 ⇒ a + b + c = 9 . Chọn đáp án D.

Đáp án B.
Ta có V = a b c S = 2 a b + b c + c a . Theo đề ta có:
a b c = 2 a b + b c + c a ; 1 ≤ a ≤ b ≤ c ⇔ 1 = 2. a b + b c + c a a b c ⇔ 2 a + 2 b + 2 c = 1
Ta có 1 = 2 a + 2 b + 2 c ≤ 2 a + 2 a + 2 a = 6 a ⇒ a ≤ 6 . Kết hợp với 2 a + 2 b + 2 c = 1 ta có:
a = 3 ⇒ 1 b + 1 c = 1 6 ⇒ 6 < b ≤ 12
⇒ a ; b ; c e { 3 ; 7 ; 42 , 3 ; 8 ; 24 , 3 ; 9 ; 18 , 3 ; 10 ; 15 , 3 ; 12 ; 12 }
Với a = 4 ⇒ 1 b + 1 c = 1 4 ⇒ 4 < b ≤ 8 ⇒ a ; b ; c ∈ 4 ; 5 ; 20 , 4 ; 6 ; 12 , 4 ; 8 ; 8
với a = 5 ⇒ 1 b + 1 c = 3 10 < 1 3 ⇒ b < 6 ⇒ a ; b ; c ∈ 5 ; 5 ; 10
với a = 6 ⇒ 1 b + 1 c = 1 3 ⇒ b ≤ 6 ⇒ a ; b ; c ∈ 6 ; 6 ; 6
⇒ a ; b ; c ∈ 3 ; 7 ; 42 , 3 ; 8 ; 24 , 3 ; 9 ; 18 , 3 ; 10 ; 15 , 3 ; 12 ; 12 4 ; 6 ; 20 , 4 ; 6 ; 12 , 4 ; 8 ; 8 , 5 ; 5 ; 10 , 6 ; 6 ; 6
Vậy ta chọn B.

Đáp án D
y ' = 4 a x 3 + 2 b x , y ' 1 = - 4 a - 2 b
Phương trình tiếp tuyến tại A là: d: y=(-4a-2b)(x+1)
Xét phương trình tương giao: a x 4 + b x 2 + c = ( - 4 a - 2 b ) ( x + 1 )
Phương trình có 2 nghiệm x=0,x=2 => 4 a + 2 b + c = 0 28 a + 10 b + c = 0 ( 1 )
∫ 0 2 - 4 a - 2 b x + 1 - a x 4 - b x 2 - c d x = - 2 a - b x 2 + - 4 a - 2 b x - a x 5 5 - b x 3 3 - c x 2 0 = - 112 5 a - 32 3 b - 2 c = 28 5 2 1 , 2 ⇒ a = 1 b = - 3 ⇒ y = x 4 - 3 x 2 + 2 , d : y = 2 x + 2 c = 2 ⇒ S = ∫ - 1 0 x 4 - 3 x 2 + 2 d x = x 5 5 - x 3 - x 2 0 - 1 = 1 5

Đáp án D

∫ 0 2 [ ( − 4 a − 2 b ) ( x + 1 ) − ax 4 − b x 2 − c ] d x = [ ( − 2 a − b ) x 2 + ( − 4 a − 2 b ) x − ax 5 5 − b x 3 3 − c x ] 2 0 = − 112 5 a − 32 3 b − 2 c = 28 5 ( 2 ) ( 1 ) , ( 2 ) ⇒ a = 1 b = − 3 c = 2 ⇒ y = x 4 − 3 x 2 + 2 , d : y = 2 x + 2 ⇒ S = ∫ − 1 0 ( x 4 − 3 x 2 + 2 ) d x = x 5 5 − x 3 − x 2 0 − 1 = 1 5

Đáp án D.

Ta có y ' = 4 a x 3 + 2 b x → y ' − 1 = − 4 a − 2 b . Phương trình tiếp tuyến của (C) tại điểm A − 1 ; 0 là đường thẳng
d : y = y ' − 1 . x + 1 ⇔ y = − 4 a − 2 b x − 4 a − 2 b
Phương trình hoành độ giao điểm của đường thẳng d và đồ thị (C) là:
a x 4 + b x 2 + c = − 4 a + 2 b x − 4 a − 2 b ⇔ a x 4 + b x 2 + 4 a + 2 b x + 4 a + 2 b + c = 0 (*)
Quan sát đồ thị, ta thấy đường thẳng d cắt đồ thị tại hai điểm có hoành độ x = 0, x = 2 nên phương trình (*) có hai nghiệm x = 0, x = 2 .
Suy ra
4 a + 2 b + c = 0 16 a + 4 b + 2 4 a + 2 b + 4 a + 2 b + c = 0 ⇔ 4 a + 2 b + c = 0 28 a + 10 b + c = 0 (1)
Diện tích hình phẳng giới hạn bởi đường thẳng d, đồ thị (C) và hai đường thẳng x = 0, x = 2 là
S = ∫ 0 2 − 4 a − 2 b x − 4 a − 2 b − a x 4 + b x 2 + c d x = 28 5
⇔ ∫ 0 2 − 4 a − 2 b x − 4 a − 2 b − a x 4 − b x 2 − c d x = 28 5
⇔ − a 5 x 5 − b 3 x 3 − 2 a + b x 2 − 4 a + 2 b + c x 0 2 = 28 5
⇔ − 32 5 a − 8 b 3 − 4 2 a + b − 2 4 a + 2 b + c = − 28 5 ⇔ 112 5 a + 32 3 b + 2 c = 28 5 ( 2 )
Giải hệ phương trình gồm (1) và (2) ta tìm được: a = − 1, b = 3, c = − 2 .
Suy ra C : y = − x 4 + 3 x 2 − 2 và d : y = − 2 x − 2 . Diện tích hình phẳng cần tính là:
S = ∫ − 1 0 − x 4 + 3 x 2 − 2 − − 2 x − 2 d x = ∫ − 1 0 − x 4 + 3 x 2 + 2 x d x = ∫ − 1 0 x 4 − 3 x 2 − 2 x d x
= x 5 5 − x 3 − x 2 − 1 0 = 1 5 (đvdt).


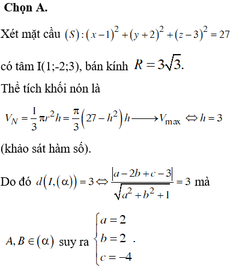
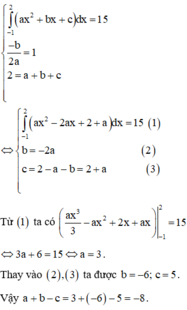



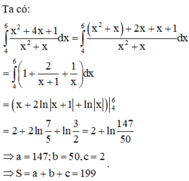
Diện tích hình tròn S = 8 π
Phương trình hoành độ giao điểm của (P) và (C) là
Suy ra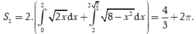
Suy ra
Chọn C.