Question

[Nguyễn Linh Nhi]

Cho phân số: B= \(\frac{10n}{5n-3}\) (n thuộc Z). Tìm giá trị lớn nhất của B

Answer 1

[Edowa Conan]

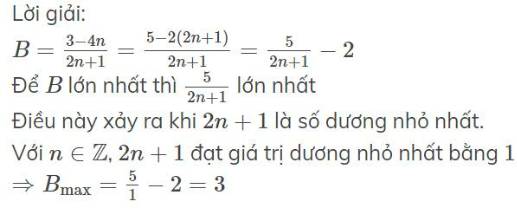
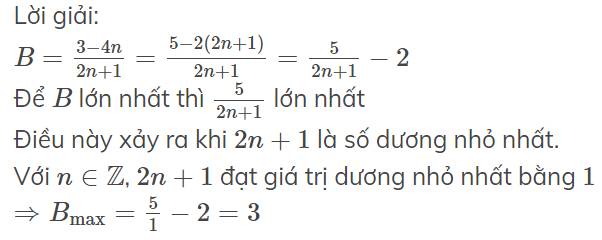
Ta có:\(\frac{10}{5n-3}=\frac{2.\left(5n-3\right)+6}{5n-3}=2+\frac{6}{n-3}\)

      Suy ra:6 chia hết cho n-3

             Hoặc n-3\(\in\)Ư(6)

Vậy Ư(6) là:(1,2,3,6)

                 Do đó ta có bảng sau:

5n-3	1	2	3	6
5n	4	5	6	9
n	ko TM	1	ko TM	ko TM

Vậy n=1

Answer 2

[Nguyễn Huy Tú]

Giải:

Để B thuộc Z thì 10n chia hết cho 5n - 3

\(10n⋮5n-3\)

\(\Rightarrow\left(10n-6\right)+6⋮5n-3\)

\(\Rightarrow2\left(5n-3\right)+6⋮5n-3\)

\(\Rightarrow6⋮5n-3\)

\(\Rightarrow5n-3\in\left\{\pm1;\pm2;\pm3;\pm6\right\}\)

+) \(5n-3=1\Rightarrow n=\frac{4}{5}\) ( loại )

+) \(5n-3=-1\Rightarrow n=\frac{2}{5}\) ( loại )

+) \(5n-3=2\Rightarrow n=1\) ( chọn )

+) \(5n-3=-2\Rightarrow n=\frac{1}{5}\) ( loại )

+) \(5n-3=3\Rightarrow n=\frac{6}{5}\) ( loại )

+) \(5n-3=-3\Rightarrow n=0\) ( chọn )

+) \(5n-3=6\Rightarrow n=\frac{9}{5}\) ( loại )

+) \(5n-3=-6\Rightarrow n=\frac{-3}{5}\) ( loại )

Vì 0 < 1 nên n = 1 để B có giá trị lớn nhất

Vậy n = 1