Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: PTHĐGĐ là:
x^2+mx-m-2=0(1)
Khi m=2 thì (1) sẽ là
x^2+2x-2-2=0
=>x^2+2x-4=0
=>\(\left[{}\begin{matrix}x=-1+\sqrt{5}\\x=-1-\sqrt{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=6-2\sqrt{5}\\y=6+2\sqrt{5}\end{matrix}\right.\)
b: Δ=m^2-4(-m-2)
=m^2+4m+8
=(m+2)^2+4>0 với mọi x
=>(d) luôn cắt (P) tại hai điểm phân biệtx
x1^2+x2^2=7
=>(x1+x2)^2-2x1x2=7
=>(-m)^2-2(-m-2)=7
=>m^2+2m+4-7=0
=>m^2+2m-3=0
=>m=-3 hoặc m=1

Lời giải:
1. PT hoành độ giao điểm:
$x^2-(2x-m^2+9)=0\Leftrightarrow x^2-2x+m^2-9=0(*)$
Khi $m=1$ thì pt trên trở thành: $x^2-2x-8=0$
$\Leftrightarrow (x-4)(x+2)=0\Rightarrow x=4$ hoặc $x=-2$
Khi $x=4\Rightarrow y=x^2=16$. Giao điểm thứ nhất là $(4,16)$
Khi $x=-2\Rightarrow y=x^2=4$. Giao điểm thứ hai là $(-2,4)$
2. $(P)$ và $(d)$ cắt nhau tại 2 điểm phân biệt $\Leftrightarrow (*)$ có 2 nghiệm phân biệt (hai nghiệm ấy chính là giá trị của 2 hoành độ giao điểm)
$\Leftrightarrow \Delta'=1-(m^2-9)>0\Leftrightarrow 10>m^2(1)$
Hai giao điểm nằm về phía của trục tung, nghĩa là 2 hoành độ giao điểm $x_1,x_2$ trái dấu. Điều này xảy ra khi $x_1x_2< 0\Leftrightarrow m^2-9< 0(2)$
Từ $(1);(2)$ suy ra $m^2-9< 0\Leftrightarrow -3< m< 3$

b. Phương trình hoành độ giao điểm:
\(x^2=4x-m\Leftrightarrow x^2-4x+m=0\) (1)
d cắt (P) tại 2 điểm phân biệt khi và chỉ khi (1) có 2 nghiệm pb
\(\Leftrightarrow\Delta'=4-m>0\Rightarrow m< 4\)
Khi đó kết hợp hệ thức Viet và điều kiện đề bài:
\(\left\{{}\begin{matrix}x_1+x_2=4\\2x_1+x_2=-5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=4\\x_1=-9\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=-9\\x_2=13\end{matrix}\right.\)
Mà \(x_1x_2=m\)
\(\Rightarrow m=-9.13=-117\)
a) Thay m=6 vào (d), ta được: y=4x-6
Phương trình hoành độ giao điểm của (P) và (d) là:
\(2x^2=4x-6\)
\(\Leftrightarrow2x^2-4x+6=0\)
\(\text{Δ}=\left(-4\right)^2-4\cdot2\cdot6=16-48=-32\)(loại)
Vì Δ<0 nên phương trình vô nghiệm
Vậy: Khi m=6 thì (P) và (d) không có điểm chung

b) (d) cắt (P) tại 2 điểm A, B phân biệt nằm về 2 phía của trục tung khi và chỉ khi
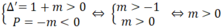
Khi đó 2 nghiệm của phương trình là:
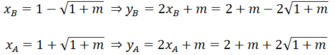
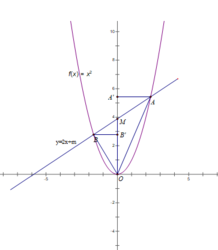
Kẻ BB' ⊥ OM ; AA' ⊥ OM
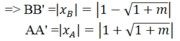
Ta có:
S A O M = 1/2 AA'.OM ; S B O M = 1/2 BB'.OM
Theo bài ra:
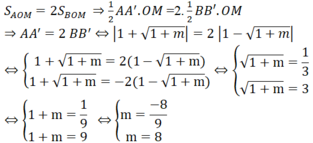
Do m > 0 nên m = 8
Vậy với m = 8 thì thỏa mãn điều kiện đề bài.

b: Thay m=2 vào (d), ta được:
y=2x-2+1=2x-1
Phương trình hoành độ giao điểm là:
\(x^2=2x-1\)
=>\(x^2-2x+1=0\)
=>(x-1)^2=0
=>x-1=0
=>x=1
Thay x=1 vào (P), ta được:
\(y=1^2=1\)
Vậy: Khi m=2 thì (P) cắt (d) tại A(1;1)
b: Phương trình hoành độ giao điểm là:
\(x^2=2x-m+1\)
=>\(x^2-2x+m-1=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot1\cdot\left(m-1\right)\)
=4-4m+4
=-4m+8
Để (P) cắt (d) tại hai điểm phân biệt thì Δ>0
=>-4m+8>0
=>-4m>-8
=>m<2
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2\\x_1x_2=\dfrac{c}{a}=m-1\end{matrix}\right.\)
y1,y2 thỏa mãn gì vậy bạn?