Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

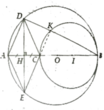
a, (O) và (I) tiếp xúc trong với nhau
b, Tứ giác ADCE là hình thoi
c, Có CK ⊥ AB, AD ⊥ DB
=> CK//AD mà CE//AD
=> B,K,D thẳng hàng
d, H K D ^ = H D K ^ ; I K B ^ = I B K ^
=> H K D ^ + I K B ^ = I B K ^ + H D K ^ = 90 0
=> I K H ^ = 90 0

a/
HC=HD (bán kính vuông góc với dây cung thì chia đôi dây cung)
HA=HE (đề bài)
=> ACED là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Mà AE vuông góc CD
=> ACED là hình thoi (Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi)
b/
Vì ACDE là hình thoi => AD=ED => tg ADE cân tại D
Mà DH vuông góc AE
=> DH là đường cao đồng thời là đường phân giác của ^ADE => ^ADC=^CDI
Ta có \(sđ\widehat{ADC}=\frac{1}{2}sđ\widebat{AC}\)(góc nội tiếp đường tròn (O))
\(sđ\widehat{ABC}=\frac{1}{2}sđ\widebat{AC}\) (góc nội tiếp đường tròn (O))
=> ^CDI=^ABC
Xét tg vuông BCH có
^ABC+^DCB=90 => ^CDI+^DCB=90 => ^CID=90=> ^EIB=90
=> I nhìn EB dưới 1 góc vuông => I thuộc đường trong đường kính EB tâm O' là trung điểm của EB
c/
Xét tg vuông CDI có \(IH=CH=DH=\frac{CD}{2}\) (trung tuyến thuộc cạnh huyền)
=> tg DHI cân tại H => ^CDI=^DIH (1)
Xét tg vuông BIE có \(IO'=EO'=BO'\) (trung tuyến thuộc cạnh huyền)
=> tg BIO' cân tại O' => ^ABC=^BIO' (2)
Mà ^CDI=^ABC (cmt) (3)
Từ (1) (2) (3) => ^DIH=^BIO'
Mà ^BIO'+^O'IE=90 => ^DIH+^O'IE=^HIO'=90 => HI vuông góc IO' => HI là tiếp tuyến của đường tròn (O') tại I
d/
Ta có OA=5 => AB=10
EO'=3=> EB=6
=> AE=AB-EB=10-6=4 => HE=2
=> HO'=HE+EO'=2+3=5
Mà IO'=EO' (cmt)=3
Xét tg vuông HIO' có
\(HI^2=HO'^2-IO'^2=5^2-3^2=16\Rightarrow HI=4\)



a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
b: ΔOCD cân tại O
mà OH là đường cao
nên H là trung điểm của CD
Xét tứ giác ACMD có
H là trung điểm chung của AM và CD
AM vuông góc với CD
Do đó: ACMD là hình thoi