Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
MC là tiếp tuyến
MA là tiếp tuyến
Do đó: MC=MA
Xét (O) có
NB là tiếp tuyến
NC là tiếp tuyến
Do đó: NB=NC
Ta có: MN=MC+CN
nên MN=MA+NB

a: Xét (O) có
MA là tiếp tuyến
MC là tiếp tuyến
Do đó: MA=MC
Xét (O) có
NC là tiếp tuyến
NB là tiếp tuyến
Do đó: NC=NB
Ta có: CM+CN=MN
nên MN=MA+NB

Ax \(\perp\) AB
By \(\perp\) AB
Suy ra: Ax // By hay AC // BD
Trong tam giác BND, ta có AC // BD
Suy ra: \(\frac{ND}{NA}=\frac{BD}{AC}\)(hệ quả định lí Ta-lét) (1)
Theo tính chất hai tiếp tuyến cắt nhau, ta có:
AC = CM và BD = DM (2)
Từ (1) và (2) suy ra: \(\frac{ND}{NA}=\frac{MD}{MC}\)
Trong tam giác ACD, ta có: \(\frac{ND}{NA}=\frac{MD}{MC}\)
Suy ra: MN // AC (theo định lí đảo định lí Ta-lét)
Mà: AC \(\perp\) AB (vì Ax \(\perp\) AB)
Suy ra: MN \(\perp\) AB
b. Trong tam giác ACD, ta có: MN // AC
Suy ra: \(\frac{MN}{AC}=\frac{DN}{DA}\) (hệ quả định lí Ta-lét) (3)
Trong tam giác ABC, ta có: MH // AC (vì M, N, H thẳng hàng)
Suy ra: \(\frac{HN}{AC}=\frac{BN}{BC}\) (hệ quả định lí Ta-lét) (4)
Trong tam giác BDN, ta có: AC // BD
Suy ra: \(\frac{ND}{NA}=\frac{BN}{NC}\) (hệ quả định lí Ta-lét)
\(\Rightarrow\frac{ND}{\left(DN+NA\right)}=\frac{BN}{\left(BN+NC\right)}\Leftrightarrow\frac{ND}{DA}=\frac{BN}{BC}\left(5\right)\)
Từ (3), (4) và (5) suy ra: MN/AC = HN/AC => MN = HN

* Theo a, ∆MON và APB đồng dạng với nhau với tỉ số đồng dạng là:
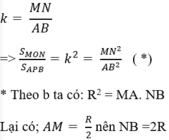
Mà: MN = MP+NP = MA+NB = R/2 +2R = 5R/2
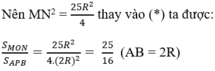

a/
Xét tg vuông OAC và tg vuông OMC có
OA=OM=R
OC chung
=> tg OAC = tg OMC (Hai tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau)
\(\Rightarrow\widehat{AOC}=\widehat{MOC}=\dfrac{\widehat{AOM}}{2}\)
Tương tự ta cũng có
tg OBD = tg OMD \(\Rightarrow\widehat{BOD}=\widehat{MOD}=\dfrac{\widehat{BOM}}{2}\)
\(\Rightarrow\widehat{MOC}+\widehat{MOD}=\widehat{COD}=\dfrac{\widehat{AOM}}{2}+\dfrac{\widehat{BOM}}{2}=\dfrac{180^o}{2}=90^o\)
b/
AB+BD nhỏ nhất khi \(M\equiv B\)

a: Xét tứ giác OBDM có
góc OBD+góc OMD=180 độ
=>OBDM là tư giác nội tiếp
c: Xét ΔKOB và ΔKFE có
góc KOB=góc KFE
góc OKB=góc FKE
=>ΔKOB đồng dạng với ΔKFE
=>KO/KF=KB/KE
=>KO*KE=KB*KF
Mình vẽ tạm trên Paint vì không biết vẽ nửa đường tròn trên đây nha '-'
Bài làm
a) Vì M là giao điểm của hai tiếp tuyến MN và Ax
=> OM là phân giác
=> \(\widehat{O_2}=\widehat{O_3}\Rightarrow2\widehat{O_2}=\widehat{HOA}\)
Vì N là giao điểm của hai tiếp tuyến MN và By
=> ON là phân giác
=> \(\widehat{O_1}=\widehat{O_4}\Rightarrow2\widehat{O_1}=\widehat{HOB}\)
Ta có: \(\widehat{HOA}+\widehat{HOB}=180^0\)(hai góc kề bù)
hay \(2\widehat{O_1}+2\widehat{O_2}=180^0\)
=> \(2\left(\widehat{O_1}+\widehat{O_2}\right)=180^0\)
=> \(\widehat{MON}=\frac{180^0}{2}=90^0\)
Vậy \(\widehat{MON}=90^0\)
b) Vì M là giao điểm của hai tiếp tuyến MN và Ax
=> AM = MH ( tính chất hai tiếp tuyến cắt nhau)
Vì N là giao điểm của hai tiếp tuyến MN và By
=> NB = NH (tính chất hai tiếp tuyến cắt nhau)
Ta có: MN = MH + NH
hay MN = AM + BN (đpcm)
c) Xét tam giác MON vuông tại O có:
OH là đường cao
Theo quan hệ giữa cạnh và đường cao
=> OH2 = MH . NH
hay R2 = MA . BN
Vậy AM . BN = R2