Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

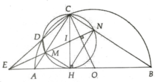
a, Tứ giác CMHN là hình chữ nhật
b, Ta có
O
C
A
^
=
O
A
C
^
C B A ^ = A C H ^ ; A C H ^ = C M N ^
=> O C A ^ + C M N ^ = 90 0
Vậy OC ⊥ MN
c, Ta có ∆IOC có E là trực tâm suy ra IN đi qua M và E (đpcm)
d, Ta có E M A ^ = C M N ^ ; C M N ^ = C B A ^ => ∆EMA:∆ENB
Tương tự ∆EMH:∆EHN => EM.EN = E H 2 ngoài ra , ∆EHC vuông tại H có HD là đường cao
=> E H 2 = ED.EC. Từ đó ta có đpcm

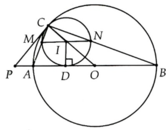
a, Vẽ tiếp tuyến tại C cắt đường AB ở P. Phân giác C P B ^ cắt OC ở I. Vẽ đường tròn tâm I bán kính IC, đó là đường tròn cần tìm
b, Do A C B ^ = 90 0 nên M C N ^ = 90 0
=> MN là đường kính của (I) => ĐPCM
c, Chứng minh được MN//AB nên ID ^ MN => M D ⏜ = N D ⏜ hay CD là tia phân giác A C B ^ => Đpcm

Chọn đáp án D
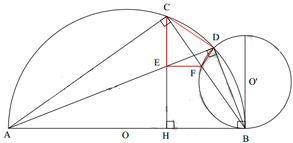

* Gọi (O’) là đường tròn đi qua D và tiếp xúc với AB tại B.
Đường tròn (O’) cắt CB tại F khác B. Chứng minh E F / / A B .
Ta có:

Hai góc ở vị trí đồng vị ⇒ E F / / A B

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
=>ΔAMB vuông tại M
Xét (O) có
ΔANB nội tiếp
AB là đường kính
=>ΔANB vuông tại N
Xét ΔCAB có
AN.BM là đường cao
AN cắt BM tại H
=>H là trực tâm
=>CH vuông góc AB
b:
Gọi giao của CH vơi AB là K
=>CH vuông góc AB tại K
góc OMI=góc OMH+góc IMH
=góc OBM+góc IHM
=góc OBM+góc BHK=90 độ
=>IM là tiếp tuyến của (O)