Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

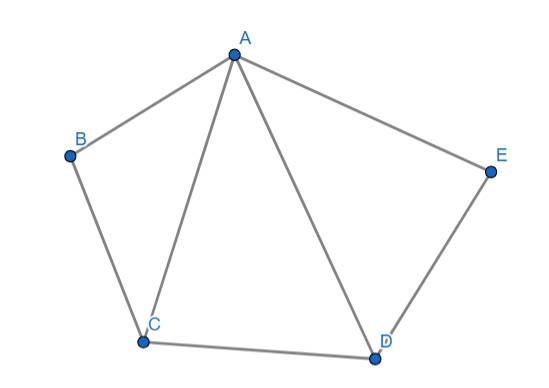
Ta có hình ngũ giác ABCDE ta có 4 cách lập vectơ có điểm cuối là điểm A
Các vectơ lập được là:
\(\overrightarrow{BA};\overrightarrow{CA};\overrightarrow{DA};\overrightarrow{EA}\)


Chọn C.
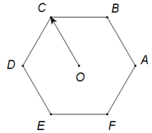
Các vecto cùng phương với ![]() có điểm đầu và điểm cuối là các đỉnh của lục giác :
có điểm đầu và điểm cuối là các đỉnh của lục giác : ![]()

* Với điểm đầu là A: Có 4 vectơ được lập ra từ các cạnh và đường chéo của ngũ giác là: A B → ; A C → ; A D → ; A E →
* Tương tự với các đỉnh còn lại.
* Do đó, số vectơ được lập ra từ các cạnh và đường chéo của ngũ giác là 4.5 = 20 vecto
Đáp án D

Vì O là tâm của ngũ giác abcde nên O cũng là trọng tâm của ngũ giác nên vecto oa+ob+oc+od+oe=0

Xét các vectơ có điểm A là điểm đầu thì có các vectơ thỏa mãn bài toán là A B → , A C → , A D → nên có 3 vectơ.
Tương tự cho các điểm còn lại B; C; D
Có tất cả: 3+ 3+ 3+ 3 =12 vecto thỏa mãn.
Chọn D.


Với hai điểm phân biệt chẳng hạn A và B , có hai vecto \(\overrightarrow{AB}\) và \(\overrightarrow{BA}\) .Với 5 điểm phân biệt đã cho , ta có 10 tập hợp khác nhau cụ thể là :
\(\left\{A,B\right\},\left\{A,C\right\},\left\{A,D\right\},\left\{A,E\right\},\left\{B,C\right\},\left\{B,D\right\},\left\{B,E\right\},\left\{C,D\right\},\left\{C,E\right\},\left\{D,E\right\}\)
Do đó ta có 20 vecto ( khác vecto 0) có điểm đầu và điểm cuối là 5 điểm đã cho.