HH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TH
1
C
3
VH
0
ND
1
2 tháng 7 2021
\(A=\left(99...96\right)^2\)
\(=\left(99...990+6\right)^2\) (100 chữ số 9)
Có \(10^{100}-1=99....99\) (100 chữ số 9)
\(\Rightarrow10^{101}-10=99...990\) ( 100 chữ số 9)
\(\Rightarrow A=\left(10^{101}-10+6\right)^2\)
\(=\left(10^{101}-4\right)^2\)\(=10^{202}-8.10^{101}+16\)
Có \(10^{202}=10.....00\) (202 chữ số 0) có tổng các chữ số là 1
\(8.10^{101}=800...00\) (101 chữ số 0) có tổng các chữ số là 8
\(16\) có tổng các chữ số là 7
\(\Rightarrow\) Tổng các chữ số của A là \(1+8+7=16\)
D
1
28 tháng 9 2021
\(n^{2}={\underbrace{999\dots 9}_{\text{50 chữ số 9}}}^{2}=\left(10^{50}-1\right)^{2}=10^{100}-2\cdot 10^{50}+1=\left(10^{50}-2\right)\cdot 10^{50}+1=\underbrace{999\dots 9}_{\text{49 chữ số 9}}8\cdot10^{50}+1=\underbrace{999\dots 9}_{\text{49 chữ số 9}}8\underbrace{000\dots 0}_{\text{49 chữ số 0}}1\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 2 2020
\(n=10^{50}-1\Rightarrow n^2=10^{100}-2.10^{50}+1=9...980...01\)
Trong đó có \(n-1\) số 9
Vậy kết quả là \(9\left(n-1\right)+8+1=9n\)
H
0
AH
Akai Haruma
Giáo viên
26 tháng 8 2021
Tất cả những vấn đề em hỏi đều thuộc lý thuyết phân tích cấu tạo số cơ bản. Tất nhiên, lời giải sẽ có 1 chút tắt (không đáng kể).
Tip: Em chịu khó viết ra nháp từng bước một và đọc kỹ. Nếu thấy số dài mà không hiểu vì sao người ta làm vậy, em thử với bộ số nhỏ hơn có phong cách tương tự (ví dụ 994009)
AH
Akai Haruma
Giáo viên
26 tháng 8 2021
\(\underbrace{999....9}_{10} 4\underbrace{000..0}_{10}9=\underbrace{999....9}_{10} 4\underbrace{00...0}_{11}+9\)
\(=\underbrace{999....9}_{10}4\times 1\underbrace{00...0}_{11}+9\)
\(=(\underbrace{999....9}_{10}7-3)\times (\underbrace{99....9}_{10}7+3)-9\)
(em tưởng tượng 1000 có 3 chữ số 0 đằng sau, biểu diễn được thành 997+3 có 3-1=2 chữ số 9)
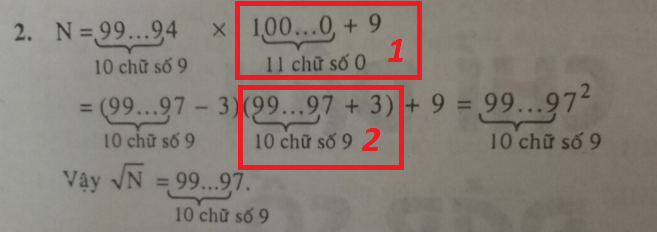
n=99...9
Tổng các chữ số của n :
n=9+9+...+9 (500 lần )
=> n= 9.500 =4500