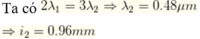Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()
Khoảng cách ngắn nhất giữa hai vân sáng cùng màu với vân trung tâm là
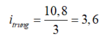
Dễ thấy 3,6 = 2.1,8 → Vị trí cùng màu vân trung tâm và gần vân trung tâm nhất ứng với vân sáng bậc 2 của λ1

Đáp án D

Đáp án: A
+ Điều kiện vân sáng của λ1 trùng với vân sáng của λ2:
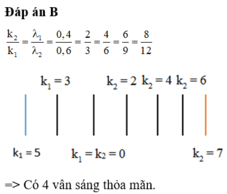
k2/k1 = λ1/λ2 = 0,42/0,56 = a/b = 3/4
+) Điều kiện vân sáng của λ1 trùng với vân sáng của λ3:
k3/k1 = λ1/λ3 = 0,42/0,63 = c/d = 2/3
+) Điều kiện vân sáng của λ2 trùng với vân sáng của λ3:
k3/k2 = λ2/λ3 = 0,56/0,63 = e/f = 8/9
→ Khoảng vân trùng i = b.d.λ1 = a.d.λ2 = b.c.λ3
hay i = 12λ1 = 9λ2 = 8λ3
Trong khoảng giữa hai vân sáng liên tiếp có màu giống màu vân trung tâm, có 2 vị trí vân sáng bức xạ 1 trùng với bức xạ 2, 3 vị trí vân sáng bức xạ 1 trùng với bức xạ 3.
=> Số vân sáng quan sát được là N = (12 – 1)+ (9 – 1) + (8 – 1) – (2 + 3) = 21 vân
(2 vân sáng trùng nhau tính là 1)

Chọn B
Ta có i1 = 1,8 mm ứng với λ = 0,6μm.
i12 = 3,6 mm => λ12 = 1,2μm.
Ở đây λ12 chỉ chia hết cho λ = 0,4μm.

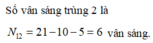
Nếu chỉ dùng ánh sáng có bước sóng λ1 thì trên đoạn MN có 10 + 6 = 16 vân sáng → MN = 15i1
Nếu chỉ dùng ánh sáng có bước sóng λ2 thì trên đoạn MN có 5 + 6 = 11 vân sáng → MN = 10i2
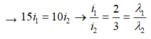
Đáp án A

Phương pháp:
Sử dụng lí thuyết về giao thoa sóng ánh sáng, điều kiện để một điểm là vị trí vân sáng
Vị trí vân sáng: x s = k λ D a
Cách giải:
+ Tại M là vị trí vân sáng bậc n của λ1 và bậc n + 1 của λ2 => nλ1 = (n +1)λ2
Hay 0,6n = 0,5(n + 1) => n = 5. Khi đó xM = 5i1
+ M còn là vị trí vân sáng của một số bức xạ khác => xM = ki = 5i1 => λ = 5λ1/k
Theo đề bài 0,38μm ≤ λ ≤ 0,76μm => 0,38μm ≤ 5λ1/k ≤ 0,76μm => 3,95 ≤ k ≤ 7,89
Do đó k: 4,5,6,7 => có tất cả 4 bức xạ cho vân sáng tại M => ngoài λ1 và λ2 thì tại M còn 2 bức xạ cho vân sáng
Chọn A