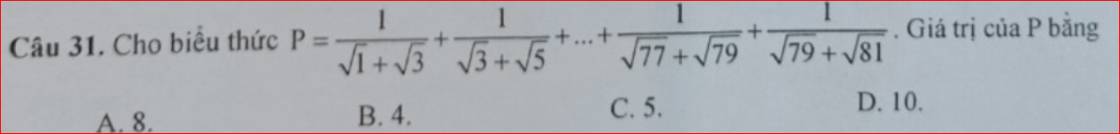K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H9
HT.Phong (9A5)
CTVHS
29 tháng 7 2023
\(P=\dfrac{1}{\sqrt{1}+\sqrt{3}}+\dfrac{1}{\sqrt{3}+\sqrt{5}}+...+\dfrac{1}{\sqrt{77}+\sqrt{79}}+\dfrac{1}{\sqrt{79}+\sqrt{81}}\)
\(P=\dfrac{\sqrt{1}-\sqrt{3}}{\left(\sqrt{1}+\sqrt{3}\right)\left(\sqrt{1}-\sqrt{3}\right)}+\dfrac{\sqrt{3}-\sqrt{5}}{\left(\sqrt{3}+\sqrt{5}\right)\left(\sqrt{3}-\sqrt{5}\right)}+...+\dfrac{\sqrt{79}-\sqrt{81}}{\left(\sqrt{79}+\sqrt{81}\right)\left(\sqrt{79}-\sqrt{81}\right)}\)
\(P=\dfrac{\sqrt{1}-\sqrt{3}}{1-3}+\dfrac{\sqrt{3}-\sqrt{5}}{3-5}+...+\dfrac{\sqrt{79}-\sqrt{81}}{79-81}\)
\(P=\dfrac{\sqrt{1}-\sqrt{3}+\sqrt{3}-\sqrt{5}+\sqrt{5}-\sqrt{7}+...+\sqrt{77}-\sqrt{79}+\sqrt{79}-\sqrt{81}}{-2}\)
\(P=\dfrac{1-9}{-2}\)
\(P=\dfrac{-8}{-2}\)
\(P=4\)
⇒ Chọn B
29 tháng 7 2023
\(P=\dfrac{\sqrt{3}-1}{2}+\dfrac{\sqrt{5}-\sqrt{3}}{2}+...+\dfrac{\sqrt{81}-\sqrt{79}}{2}\)
\(=\dfrac{-1+\sqrt{3}-\sqrt{3}+\sqrt{5}-...-\sqrt{79}+9}{2}=\dfrac{8}{2}=4\)
11 tháng 11 2021
\(\Leftrightarrow n^5+n^2-n^2+1⋮n^3+1\)
\(\Leftrightarrow-n^3+n⋮n^3+1\)
\(\Leftrightarrow n=1\)
DH
So sánh :
cos 35 độ và tan 55 độ
sin 72 độ và cot 18 độ
. Giải chi tiết nha, mình cần lời giải gấp >.<
2
18 tháng 7 2017
ta có \(sina< tana\\ cosa< cota\)
mà 2 góc 35 độ và 55 độ là hai góc phụ nhau nên \(cos35^o=sin55^o< tan55^o\)
tương tự: \(sin72^o=Cos12^o< cot12^o\)
5 tháng 1 2022
a: BC=10cm
AH=4,8cm
b: Xét (A;AH) có
BC⊥AH tại H
nen BC là tiếp tuyến của (A;AH)
KV
26 tháng 5 2023
a) 2y + 3x = -4 (1)
x - y = 7 (2)
(2) ⇔ x = y + 7 thế vào (1) ta được:
2y + 3(y + 7) = -4
⇔ 2y + 3y + 21 = -4
⇔ 5y = -4 - 21
⇔ 5y = -25
⇔ y = -5
Thế y = -5 vào (2) ta được:
x - (-5) = 7
⇔ x + 5 = 7
⇔ x = 2
Vậy S = {(2; -5)}
b) ĐKXĐ: m ≠ 1/2
Thay tọa độ điểm A(-1; 3) vào (d) ta được:
(2m - 1).(-1) + m = 3
⇔ -2m + 1 + m = 3
⇔ -m = 3 - 1
⇔ -m = 2
⇔ m = -2 (nhận)
Vậy m = -2 thì (d) đi qua A(-1; 3)
Y
26 tháng 5 2023
Chu vi đáy của viên phấn là \(3,14cm\)
Ta có : \(C=R.2.3,14=R.6,28\Rightarrow R=\dfrac{C}{6,28}=\dfrac{3,14}{6,28}=0,5\left(cm\right)\)
Thể tích của 1 viên phấn là :
\(V=3,14.R^2.h=3,14.0,5^2.12=9,42\left(cm^3\right)\)
Thể tích của 20 viên phấn là : \(9,42.20=188,4\left(cm^3\right)\)
Phần không gian bên trong hộp là :
\(200-188,4=11,6\left(cm^3\right)\)
4 tháng 3 2023
a: Xét tứ giác SAOB có
góc SAO+góc SBO=180 độ
=>SAOB nội tiếp
b: Xét ΔSAK và ΔSCA có
góc SAK=góc SCA
góc ASK chung
=>ΔSAK đồng dạng với ΔSCA
=>SA/SC=SK/SA
=>SA^2=SK*SC
c: ΔOCK cân tại O
mà OI là trung tuyến
nên OI vuông góc CK
góc OIS=góc OAS=góc OBS=90 độ
=>O,I,A,S,B cùng thuộc 1 đường tròn
d: Xét ΔSAH và ΔSOA có
góc SAH=góc SOA
góc S chung
=>ΔSAH đồng dạng với ΔSOA
=>SA/SO=SH/SA
=>SA^2=SH*SO=SK*SC
4 tháng 3 2023
e: SH*SO=SK*SC
=>SH/SC=SK/SO
=>ΔSHK đồng dạng với ΔSCO
=>góc SHK=góc SCO
=>góc KHO+góc KCO=180 độ
=>OHKC nội tiếp
f: Xét ΔSAJ và ΔSIA có
góc SAJ=góc SIA
góc ASJ chung
=>ΔSAJ đồng dạng với ΔSIA
=>SA/SI=SJ/SA
=>SA^2=SI*SJ=SC*SK
26 tháng 5 2021
Ta có
\(a^2+1=a^2+ab+bc+ca=a\left(a+b\right)+c\left(a+b\right)=\left(a+b\right).\left(a+c\right)\\ Cmtt:b^2+1=\left(b+a\right).\left(b+c\right)\\ c^2+1=\left(c+a\right).\left(c+b\right)\)
Nên
\(\dfrac{b-c}{a^2+1}+\dfrac{c-a}{b^2+1}+\dfrac{a-b}{c^2+1}\\ =\dfrac{\left(b-c\right)}{\left(a+b\right)\left(a+c\right)}+\dfrac{\left(c-a\right)}{\left(b+c\right)\left(b+a\right)}+\dfrac{\left(a-b\right)}{\left(c+a\right)\left(c+b\right)}\\ =\dfrac{\left(b-c\right)\left(b+c\right)+\left(c-a\right)\left(c+a\right)+\left(a-b\right)\left(a+b\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\\ =\dfrac{b^2-c^2+c^2-a^2+a^2-b^2}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\\ =0\)
26 tháng 5 2021
\(\dfrac{b-c}{a^2+1}+\dfrac{c-a}{b^2+1}+\dfrac{a-b}{c^2+1}\)
\(=\dfrac{b-c}{a^2+ab+bc+ac}+\dfrac{c-a}{b^2+ab+bc+ca}+\dfrac{a-b}{c^2+ab+bc+ca}\)
\(=\dfrac{b-c}{a\left(a+b\right)+c\left(a+b\right)}+\dfrac{c-a}{b\left(a+b\right)+c\left(a+b\right)}+\dfrac{a-b}{c\left(c+a\right)+b\left(a+c\right)}\)
\(=\dfrac{b-c}{\left(a+c\right)\left(a+b\right)}+\dfrac{c-a}{\left(b+c\right)\left(a+b\right)}+\dfrac{a-b}{\left(b+c\right)\left(a+c\right)}\)
\(=\dfrac{\left(b-c\right)\left(b+c\right)+\left(c-a\right)\left(a+c\right)+\left(a-b\right)\left(a+b\right)}{\left(a+c\right)\left(a+b\right)\left(b+c\right)}\)
\(=\dfrac{b^2-c^2+c^2-a^2+a^2-b^2}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=0\)