
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left|2x-3\right|=3-2x\)
\(ĐK:x\le\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)
Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)

=>3(x-1)-2(x-2)<=6/4(x-3)
=>3x-3-2x+4<=3/2x-9/2
=>-1/2x<=-9/2-1=-11/2
=>x>=11

bai 1
cho x>0, y>0 thoa man x+y\(\le\)1
cmr \(\frac{1}{x}\)+\(\frac{1}{y}\)\(\ge\)\(\frac{4}{x+y}\)
bai 2
tim a
m=\(\frac{a^{2^{ }}+a+1}{a}\): *(a+1)+\(\frac{1}{a}\)
mk chi co 2 bai thoi
chuc bn hoc tot![]()

\(P=\left(x+\dfrac{1}{x}\right)^2+\left(y+\dfrac{1}{y}\right)^2+\left(z+\dfrac{1}{z}\right)^2-\left(x+\dfrac{1}{x}\right)\left(y+\dfrac{1}{y}\right)\left(z+\dfrac{1}{z}\right)\)
Ta có: \(xyz=1\Rightarrow x=\dfrac{1}{yz}\)
\(P=\left(\dfrac{1}{yz}+yz\right)^2+\left(y+\dfrac{1}{y}\right)^2+\left(z+\dfrac{1}{z}\right)^2-\left(yz+\dfrac{1}{yz}\right)\left(y+\dfrac{1}{y}\right)\left(z+\dfrac{1}{z}\right)\)
\(P=\dfrac{1}{y^2z^2}+2+1y^2z^2+y^2+2+\dfrac{1}{y^2}+z^2+2+\dfrac{1}{z^2}-\left(y^2z+z+\dfrac{1}{z}+\dfrac{1}{y^2z}\right)\left(z+\dfrac{1}{z}\right)\)
\(P=\dfrac{1}{y^2z^2}+y^2z^2+y^2+\dfrac{1}{y^2}+z^2+\dfrac{1}{z^2}+6-y^2z^2-y^2-z^2-1-1-\dfrac{1}{z^2}-\dfrac{1}{y^2}-\dfrac{1}{y^2z^2}\)\(P=\left(\dfrac{1}{y^2z^2}-\dfrac{1}{y^2z^2}\right)+\left(y^2z^2-y^2z^2\right)+\left(y^2-y^2\right)+\left(z^2-z^2\right)+\left(\dfrac{1}{y^2}-\dfrac{1}{y^2}\right)+\left(\dfrac{1}{z^2}-\dfrac{1}{z^2}\right)+4\)
\(P=4\)
Vậy: ...

\(c2:3x+5x^2\ge-6+5x+5x^2\Leftrightarrow2x-6\le0\Leftrightarrow x\le3\)
\(c3:-x+7=6a-1\Leftrightarrow x=-\left(6a-1-7\right)=8-6a>0\Leftrightarrow a< \dfrac{4}{3}\)
\(c4:pt\Leftrightarrow\left(2019-x\right)^3+\left(2021-x\right)^3+\left[2x-4040\right]^3=0\left(1\right)\)
\(đặt:\left[\left(2019-x\right);\left(2021-x\right)\right]=\left\{u;v\right\}\)
\(\Rightarrow2x-4040=x-2019+x-2021=-u-v\)
\(\left(1\right)\Leftrightarrow u^3+v^3+\left(-u-v\right)^3=0\Leftrightarrow-3uv\left(u+v\right)=0\Leftrightarrow\left[{}\begin{matrix}u.v=0\\u=-v\end{matrix}\right.\)
\(u.v=0\Leftrightarrow\left[{}\begin{matrix}u=0\Leftrightarrow2019-x=0\Leftrightarrow x=2019\\v=0\Leftrightarrow2021-x=0\Leftrightarrow x=2021\end{matrix}\right.\)
\(u=-v\Leftrightarrow2019-x=x-2021\Leftrightarrow x=2020\)
\(\Rightarrow S=\left\{2019;2020;2021\right\}\)
Câu 2 :
\(\Leftrightarrow3x+5x^2+6-5x-5x^2\ge0\Leftrightarrow-2x+6\ge0\Leftrightarrow x\le3\)
Câu 4 :
PT <=> \(2019-x+2021-x+2x-4040=0\Leftrightarrow2019+2021-4040=0\)
( đúng )
Vậy pt có vô số nghiệm

bn nên lên hs ông Google ý chứ tháng 12 chả ai thi hsg đâu (trừ lớp 9):)))

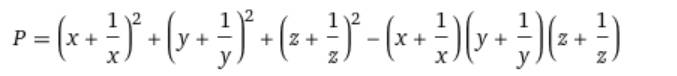



Đăng nhỏ ra em !