Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải thích: Đáp án C
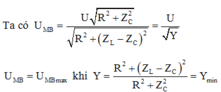
Đạo hàm theo ZC và lấy Y’ = 0, ta có: ![]()
Ta thấy ![]()
Theo đề bài:
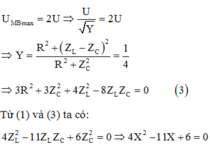
Giải phương trình có 2 nghiệm và dùng điều kiện (2) ta có:
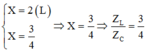

Đáp án C
Khi ω = ω1 thì 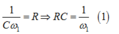
Khi ω = ω2 thì 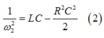
Khi ω = ω0 thì
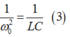
Thay (1) và (3) và (2) ta thu được 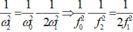

Đáp án B
Phương pháp: sử dụng giản đồ vectơ trong dòng điện xoay chiều
Cách giải:
+ Khi xảy ra cực đại của điện áp hiệu dụng trên cuộn dây, ta có u vuông pha với uRC.
Mặc khác
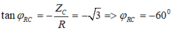
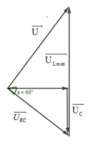
+ Từ hình vẽ, ta thấu rằng điện áp hai đầu điện trở lệch pha 300 so với điện áp hai đầu mạch.

Ta có cos φ R C = R R 2 + Z C 2 = 1 2 ⇒ φ R C = 60 0
Mặc khác khi xảy ra cực đại trên U L thì u vuông pha với u R C → φ = 30 độ.
Đáp án A
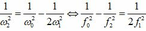
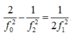
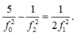
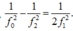
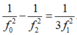


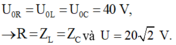
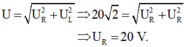
Chọn A
Ta có : UMB = U R 2 + Z C 2 R 2 + ( Z L - Z C ) 2 = U Y
UMB = UMBmax khi R 2 + ( Z L - Z C ) 2 R 2 + Z C 2 = Ymin => Đạo hàm theo ZC: Y’ = 0
⇒ R 2 - Z C 2 + ZLZC=0 => R2 = Z C 2 - ZLZC (*)
Ta thấy R2 > 0 => Z L < ZC hay Z L Z C = X <1 (**)
UMBmax = 2U => U Y = 2U => Y = R 2 + ( Z L - Z C ) 2 R 2 + Z C 2 = 1 4
⇒ 3 R 2 + 3 Z C 2 + 4 Z L 2 - 8 Z L - Z C =0(***)
Từ (*) và (***) suy ra : 4 Z L 2 - 11 Z L Z C + 6 Z C 2 =0
⇒ 4X2 -11X + 6 =0
Phương trình có hai nghiệm X=2>1(loại)
và X= 3 4 => Z L Z C = 3 4