Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
5.
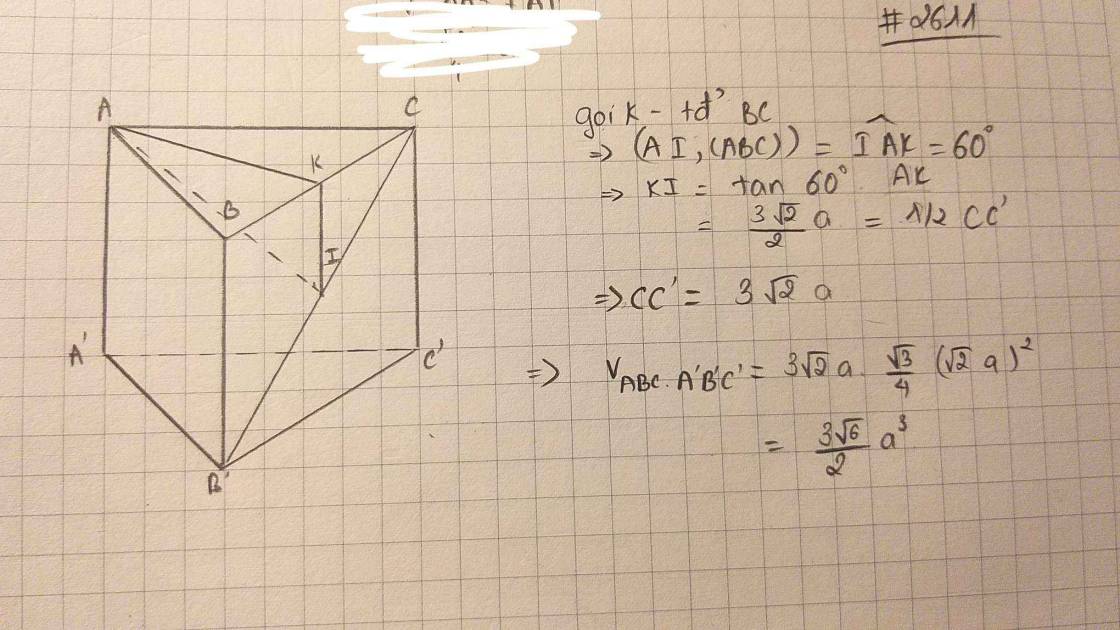
Gọi M là trung điểm BC \(\Rightarrow AM\perp BC\)
\(\Rightarrow BC\perp\left(A'AM\right)\)
\(\Rightarrow\widehat{A'MA}\) là góc giữa (A'BC) và (ABC)
\(\Rightarrow\widehat{A'MA}=60^0\)
\(AM=\frac{a\sqrt{3}}{2}\Rightarrow A'A=AM.tan60^0=\frac{3a}{2}\)
\(B=\frac{a^2\sqrt{3}}{4}\Rightarrow V=B.A'A=\frac{3\sqrt{3}}{8}a^3\)
1.
\(V=Bh\)
2.
\(B=\frac{a^2\sqrt{3}}{4}\Rightarrow V=Bh=\frac{a^2\sqrt{3}}{4}.a\sqrt{6}=\frac{3\sqrt{2}}{4}a^3\)
3.
\(B=\frac{1}{2}\left(a\sqrt{2}\right)^2=a^2\Rightarrow V=Bh=a^2.5a=5a^3\)
4.
\(h=\sqrt{\left(2a\right)^2-\left(a\sqrt{3}\right)^2}=a\)
\(B=\frac{\left(a\sqrt{3}\right)^2\sqrt{3}}{4}=\frac{3\sqrt{3}}{4}a^2\)
\(V=Bh=\frac{3\sqrt{3}}{4}a^3\)
Chọn B
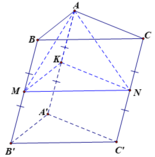
Gọi K là trung điểm của AA' và V, VABC.KMN, VA.KMN lần lượt là thể tích khối lăng trụ ABC. A'B'C' khối lăng trụ ABC. KMN và thể tích khối chóp A. MNK. Khi đó
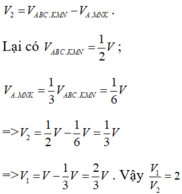
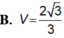
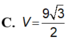
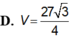
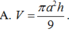
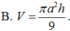
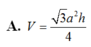
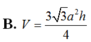
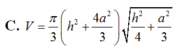
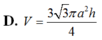
Phương pháp:
- Thể tích khối trụ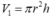
với r là bán kính đáy.
- Tính thể tích khối lăng trụ V 2 = Sh với S là diện tích đáy.
Cách giải:
Diện tích tam giác đáy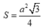
Chiều cao tam giác ABC là h = a 3 2
=> bán kính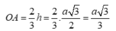
Thể tích khối trụ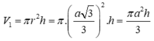
Thể tích lăng trụ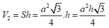
Vậy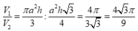
Chọn: A