Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

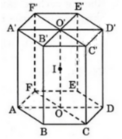
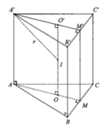
Gọi I là trung điểm của OO'
ABCDEF.A'B'C'D'E'F' là hình lăng trụ lục giác đều nên I là tâm đối xứng của các hình chữ nhật ADD'A', BEE'B', CFF'C'. Vậy nếu mp(P) đi qua I và cắt các cạnh AA', BB', CC', DD', EE', FF' theo thứ tự tại các điểm M, N, P, Q, R, S thì I là trung điểm của MQ, NR và PS
Suy ra phép đối xứng qua điểm I biến ABCDEF.MNPQRS thành D'E'F'A'B'C'.QRSMNP.
Nghĩa là ABCDEF.MNPQRS và D'E'F'A'B'C'. QRSMNP là hai khối da điện bằng nhau.
Vậy hai khối đa diện nói trên có thể tích bằng nhau.

Đáp án B
Ta có mặt bên là hình chữ nhật có diện tích bằng 3 a 2
⇒ chiều cao của lăng trụ là 3 a 2 a = 3 a .
Có diện tích đáy hình trụ bằng S = πa 2
Vậy V = 3 a . πa 2 = 3 πa 2 .

Đáp án A
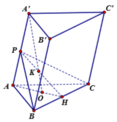
Gọi H là trung điểm của BC, giao điểm của (P) và A A ' là P.
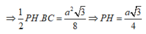

∆ A H P vuông tại P có A P = A H 2 - P H 2 = 3 a 4
∆ A A ' O ~ ∆ A H P ⇒ A ' O A O = H P A P
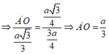
⇒ V A B C . A ' B ' C ' = O A ' . S A B C = a 3 3 12

Đáp án D
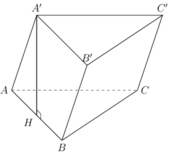
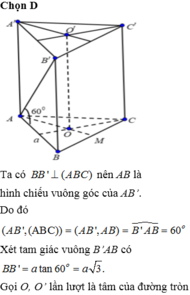
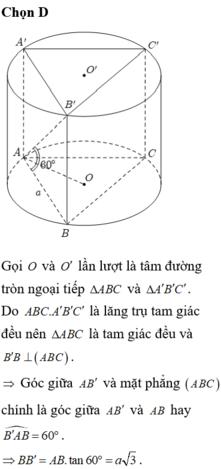
Ta có góc giữa cạnh bên AA' với mặt đáy (ABC) là:
góc A ' A H ^ và tan A ' A H = A ' H A H
Suy ra A ' H = a 2 . tan 30 ° = a 3 6
Do đó V = A ' H . S A B C = a 3 6 . a 2 3 4 = a 3 8

Thể tích của hình lăng trụ đã cho: V = \(\dfrac{a^2\sqrt{3}}{4}\).a = \(\dfrac{a^3\sqrt{3}}{4}\).
Tổng diện tích các mặt bên (diện tích xung quanh) của lăng trụ: Sxq = 3a.a = 3a2.


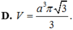

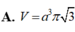

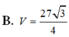
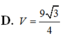

chịu chịu ok
tui ko bít