Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có mặt bên là hình chữ nhật có diện tích bằng 3 a 2
⇒ chiều cao của lăng trụ là 3 a 2 a = 3 a .
Có diện tích đáy hình trụ bằng S = πa 2
Vậy V = 3 a . πa 2 = 3 πa 2 .

Đáp án A
Gọi H là trung điểm của BC, giao điểm của (P) và A A ' là P.
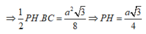

∆ A H P vuông tại P có A P = A H 2 - P H 2 = 3 a 4
∆ A A ' O ~ ∆ A H P ⇒ A ' O A O = H P A P
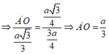
⇒ V A B C . A ' B ' C ' = O A ' . S A B C = a 3 3 12

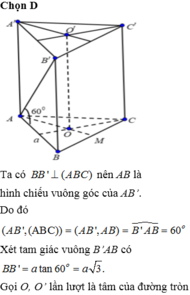
Đáp án D
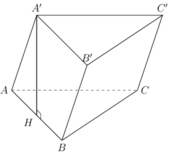
Ta có góc giữa cạnh bên AA' với mặt đáy (ABC) là:
góc A ' A H ^ và tan A ' A H = A ' H A H
Suy ra A ' H = a 2 . tan 30 ° = a 3 6
Do đó V = A ' H . S A B C = a 3 6 . a 2 3 4 = a 3 8

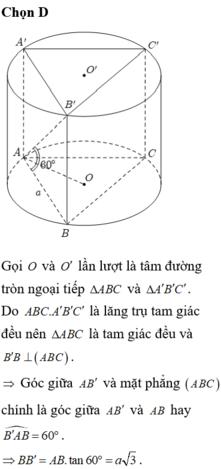
Thể tích của hình lăng trụ đã cho: V = \(\dfrac{a^2\sqrt{3}}{4}\).a = \(\dfrac{a^3\sqrt{3}}{4}\).
Tổng diện tích các mặt bên (diện tích xung quanh) của lăng trụ: Sxq = 3a.a = 3a2.
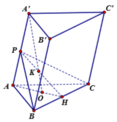





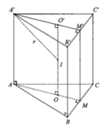
Gọi I là trung điểm của OO'
ABCDEF.A'B'C'D'E'F' là hình lăng trụ lục giác đều nên I là tâm đối xứng của các hình chữ nhật ADD'A', BEE'B', CFF'C'. Vậy nếu mp(P) đi qua I và cắt các cạnh AA', BB', CC', DD', EE', FF' theo thứ tự tại các điểm M, N, P, Q, R, S thì I là trung điểm của MQ, NR và PS
Suy ra phép đối xứng qua điểm I biến ABCDEF.MNPQRS thành D'E'F'A'B'C'.QRSMNP.
Nghĩa là ABCDEF.MNPQRS và D'E'F'A'B'C'. QRSMNP là hai khối da điện bằng nhau.
Vậy hai khối đa diện nói trên có thể tích bằng nhau.