Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

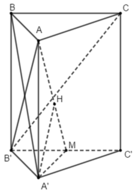
+ Gọi M là trung điểm của B’C’
Tam giác AB’C’ cân tại A ⇒ AM ⊥ B’C’
Tam giác A’B’C’ cân tại A’ ⇒ A’M ⊥ B’C’
Mà (AB’C’) ∩ (A’B’C’) = B’C’
Do đó góc giữa hai mặt phẳng (AB’C’) và (A’B’C’) là góc giữa 2 đường thẳng AM và A’M và chính là góc AMA’ ⇒ A M A ' ^ = 60 °
Ta có: A’M = 1/2 A’C’ = a/2 ⇒ AA’ = A’M. tan 60 ° = a 3 2
+ Ta có BC // (AB’C’) ⇒ d(BC; (AB’C’)) = d(B; (AB’C’))
Ta chứng minh được d(B; (AB’C’)) = d(A’; (AB’C’))
Do đó: d(BC; (AB’C’)) = d(A’; (AB’C’))
+ Ta chứng minh được (AA’M) ⊥ (AB’C’), trong mặt phẳng (AA’M), dựng A’H ⊥ AM tại H
⇒ A’H ⊥ (AB’C’) ⇒ d(A’; (AB’C’)) = A’H ⇒ d(BC; (AB’C’)) = A’H
+ Tính A’H
Ta có: 1 A ' H 2 = 1 A A ' 2 + 1 A ' M 2 ⇒ A’H = a 3 4
Vậy d(BC; (AB’C’)) = a 3 4 .
Đáp án B

a.
\(\left\{{}\begin{matrix}BB'\perp\left(ABC\right)\Rightarrow BB'\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(ABB'A'\right)\)
\(\Rightarrow BC=d\left(C;\left(A'AB\right)\right)\)
\(S_{A'AB}=\dfrac{1}{2}S_{ABB'A'}=\dfrac{3a^2}{2}\)
\(\Rightarrow V_{C.A'AB}=\dfrac{1}{3}BC.S_{A'AB}=\dfrac{1}{3}.2a.\dfrac{3a^2}{2}=a^3\)
b.
Theo cmt, \(BC\perp\left(ABB'A'\right)\Rightarrow BC\perp AN\)
Mà \(\left\{{}\begin{matrix}A'C\perp\left(P\right)\\AN\in\left(P\right)\end{matrix}\right.\) \(\Rightarrow AN\perp A'C\)
\(\Rightarrow AN\perp\left(A'BC\right)\Rightarrow AN\perp A'B\)
c.
Ta có: \(AA'||BB'\Rightarrow d\left(B;AA'\right)=d\left(N;AA'\right)\)
\(\Rightarrow S_{A'AN}=S_{A'AB}\)
Lại có: \(CC'||BB'\Rightarrow CC'||\left(ABB'A'\right)\)
\(\Rightarrow d\left(C';\left(ABB'A'\right)\right)=d\left(M;\left(ABB'A'\right)\right)\)
\(\Rightarrow V_{A'AMN}=V_{CA'AB}=a^3\)
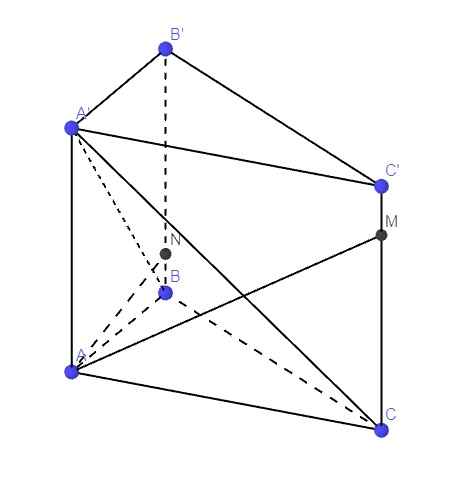
Em kiểm tra lại đề \(BC\) cắt \(\left(AB'C\right)\) tại C nên giữa chúng ko có khoảng cách
Hay là mặt phẳng \(\left(AB'C'\right)\)?