Question

[Pham Trong Bach]

Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác cân, AB = AC = a, B A C ^ = 120 ° . Mặt phẳng (AB’C’) tạo với đáy góc 60 ° . Tính khoảng cách từ đường thẳng BC đến mặt phẳng (AB’C’) theo a.

A.a/3

B.  a 3 4

C.  a 3 8

D. 5 a 3

Answer 1

[Cao Minh Tâm]

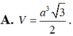
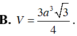
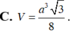
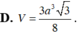
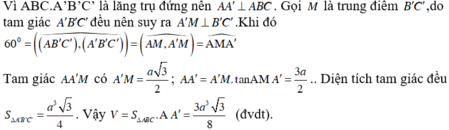
+ Gọi M là trung điểm của B’C’

Tam giác AB’C’ cân tại A ⇒ AM ⊥ B’C’

Tam giác A’B’C’ cân tại A’ ⇒ A’M  ⊥ B’C’

Mà (AB’C’) ∩  (A’B’C’) = B’C’

Do đó góc giữa hai mặt phẳng (AB’C’) và (A’B’C’) là góc giữa 2 đường thẳng AM và A’M và chính là góc AMA’ ⇒ A M A ' ^ = 60 °  

Ta có: A’M = 1/2 A’C’ = a/2 ⇒  AA’ = A’M. tan 60 ° =  a 3 2

+ Ta có BC // (AB’C’) ⇒ d(BC; (AB’C’)) = d(B; (AB’C’))

Ta chứng minh được d(B; (AB’C’)) = d(A’; (AB’C’))

Do đó: d(BC; (AB’C’)) = d(A’; (AB’C’))

+ Ta chứng minh được (AA’M) ⊥ (AB’C’), trong mặt phẳng (AA’M), dựng A’H  ⊥  AM tại H

⇒ A’H  ⊥ (AB’C’) ⇒ d(A’; (AB’C’)) = A’H ⇒  d(BC; (AB’C’)) = A’H

+ Tính A’H

Ta có: 1 A ' H 2 = 1 A A ' 2 + 1 A ' M 2 ⇒ A’H =  a 3 4

Vậy d(BC; (AB’C’)) = a 3 4 .

Đáp án B