Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em tham khảo tại link dưới đây nhé.
Câu hỏi của Linhllinh - Toán lớp 9 - Học toán với OnlineMath
Do Ax⊥ABAx⊥AB
By⊥ABBy⊥AB
⇒Ax∥By⇒Ax∥By
(Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song với nhau)
b) Xét ΔOACΔOAC và ΔOBKΔOBK có:
ˆOAC=ˆOBK=90oOAC^=OBK^=90o
OA=OBOA=OB (do O là trung điểm của AB)
ˆAOC=ˆBOKAOC^=BOK^ (đối đỉnh) và BK=ACBK=AC
⇒ΔOAC=ΔOBK⇒ΔOAC=ΔOBK (g.c.g)
⇒OC=OK⇒OC=OK (hai cạnh tương ứng)
Ta có OD⊥⊥CK và OD đi qua O là trung điểm của CK nên ODOD là đường trung trực của CKCK (đường trung trực của một đoạn thẳng là đường vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó)
c) Do OD là đường trung trực của đoạn CK nên DC=DKDC=DK (tính chất)
Mà DK=DB+BK=DB+ACDK=DB+BK=DB+AC
⇒CD=DB+AC⇒CD=DB+AC (đpcm)

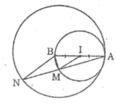
Tam giác AMB nội tiếp trong đường tròn (I) có AB là đường kính nên ![]()
Suy ra: AM ⊥ BM hay BM ⊥ AN
Suy ra: AM = MN (đường kính vuông góc dây cung).


a, Chỉ ra |OI – OK| < IK < OI + OK => (1) và (k) luôn cắt nhau
b, Do OI=NK, OK=IM => OM=ON
Mặt khác OMCN là hình chữ nhật => OMCN là hình vuông
c, Gọi{L} = KB ∩ MC, {P} = IBNC => OKBI là Hình chữ nhật và BNMI là hình vuông
=> ∆BLC = ∆KOI
=> L B C ^ = O K I ^ = B I K ^
mà B I K ^ + I B A ^ = 90 0
L B C ^ + L B I ^ + I B A ^ = 180 0
d, Có OMCN là hình vuông cạnh a cố định
=> C cố định và AB luôn đi qua điểm C

Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
=> BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE.
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
=>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
(Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/
(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
=> ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).

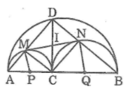
Gọi O là trung điểm của AB
Tứ giác CMDN là hình chữ nhật nên CD = MN
Trong tam giác OCD ta có: CD ≤ OD nên MN ≤ OD
Vì OD không đổi nên MN = OD là giá trị lớn nhất khi và chỉ khi C trùng với O
Vậy C là trung điểm của AB thì MN có độ dài lớn nhất.



