Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: M là hình chiếu của D trên BC
a: Xét ΔCMD vuông tại M và ΔCAB vuông tại A có
góc C chung
=>ΔCMD đồng dạng với ΔCAB
=>CM/CA=CD/CB
=>CM*CB=CA*CD
c: góc DMB+góc DAB=180 độ
=>DMBA nội tiếp
=>góc CBD=góc CAM

a: BC^2=AB^2+AC^2
=>ΔABC vuông tại A
Xét ΔNBM và ΔABC có
BN/BA=BM/BC
góc B chung
=>ΔNBM đồng dạng với ΔABC
b: ΔNBM đồng dạng với ΔABC
=>NM/AC=BM/BC
=>NM/4=2,5/5=1/2
=>NM=2cm

a: Xét ΔAND và ΔABM có
góc A chung
AN=DM
AB=AD
=>ΔAND=ΔABM
=>AN=AM
góc NAD=góc BAM
=>góc NAD+góc DAM=góc DAM+góc BAM=90 độ
=>góc NAM=90 độ
=>ΔNAM vuông cân tại A
b: Xét ΔABM và ΔPDA có
góc B=góc D
góc BAM=góc APD
=>ΔABM đồng dạng với ΔPDA
=>AB/BM=PD/AD
=>AB*AD=BM*PD=BC^2
c: Xét ΔAIH và ΔAQD có
góc A chung
góc H=góc D
=>ΔAIH đồng dạng với ΔAQD
=>AI*AD=AH*AQ
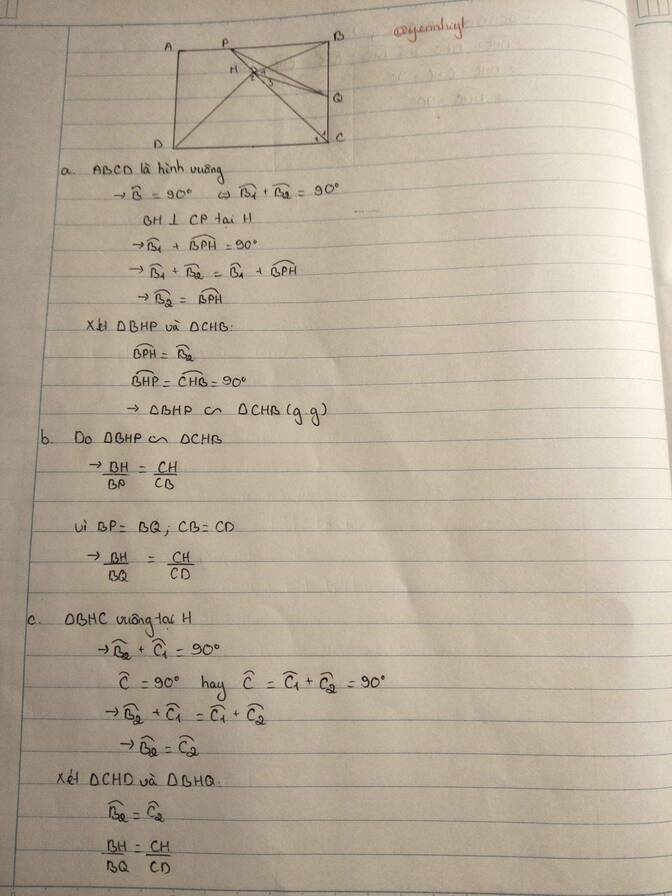
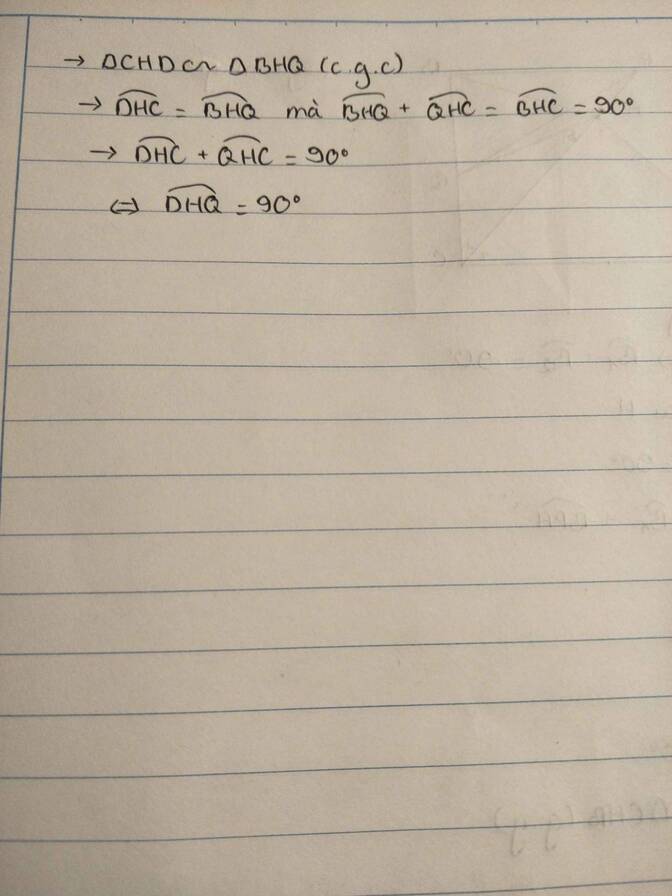
Bạn tự vẽ hình nha
a , Có BH vuông góc với MC nen tam giác BHC vuông tại H suy ra góc BHC = 90 độ suy ra góc HCB + góc HBC = 90 độ
Có góc ABC = 90 độ ( hình vuông ABCD ) . Có góc MBH + góc HBC = góc ABC = 90 độ
Suy ra góc MBH = góc BCH ( cùng phụ với góc HBC )
Xét tam giác MHB và tam giác BHC có :
Góc MHB = Góc BHC ( = 90 độ )
Góc MBH = góc BCH ( c.m.t)
Suy ra tam giác MHB đồng dạng với tam giác BHC ( g.g )
Suy ra BH/HC= HM / HB hay BH/HM = HC/ BH
Suy ra BH^2 = HM . HC
Mink chứng minh tiêp câu b nha
Có BH ^2 = HM . HC
BH ^2 = 4 .9
BH ^2 = 36
BH = 6 cm
Có tam giác BHM vuông tại M
MH2 + HB2 = MB 2 ( định lý py ta go )
4^2 + 6^2 = MB^2
16 + 36 = MB ^2
MB^2 = 52
MB = Căn 52
mà MB = BN
suy ra BN = Căn 52