Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔACE có
CD là đường trung tuyến
CD là đường cao
CD=AE/2
Do đó: ΔACE vuông tại C

a: Xét ΔCAE có
CD là đường cao
CD là trung tuyến
CD=AE/2
Do đó:ΔCAE vuông cân tại C
b: Xét ΔHAB có HI/HA=HK/HE
nên IK//AE và IK=1/2AE
=>IK=AD=BC
Xét tứ giác BIKC có
IK//BC
IK=BC
Do đó: BIKC là hình bình hành

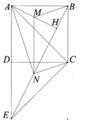
a) E là điểm đối xứng của điểm A qua điểm D Þ A, D, E thẳng hàng và DA = DE Þ CD ^ AE tại trung điểm của AE Þ CA = CE Þ DCAE cân ở C.
Þ D A C ^ = 450 Þ DACE vuông cân.
b) Áp dụng tính chất đường trung bình cho DHAE và giả thiết ABCD là hình vuông ta sẽ chứng minh được tứ giác BMNC là hình bình hành.
c) Do AH ^ BN, mà NM//CB Þ NM ^ AB nên M là trực tâm của tam giác ANB.
d) M là trực tâm DABN nên BM ^ AN mà BM//CN Þ A N C ^ = 900

a: Xét ΔACE có
CD là đường trung tuyến
CD là đường cao
CD=AE/2
Do đó: ΔACE vuông cân tại C