Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Diện tích toàn phần của hình lập phương là
![]()
Hình trụ có bán kính đáy là 20 cm và đường cao là 40 cm nên diện tích toàn phần của hình trụ là
![]()
![]()

a) Diện tích hình vuông ban đầu bằng 1.1 = 1 (đvdt)
Vì người ta nối các trung điểm của cạnh hình vuông để tạo ra hình vuông mới nên diện tích hình mới sẽ bằng một nửa hình trước.
Do đó ta có \({u_1} = {S_1} = 1,q = \frac{1}{2}\)
Vậy \({S_n} = 1.\frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{1 - \frac{1}{2}}} = {\left( {\frac{1}{2}} \right)^{n - 1}}\)
b) \(S = \frac{1}{{1 - \frac{1}{2}}} = 2\)

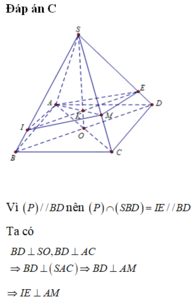
Đáp án C
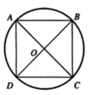
Do hình trụ và hình lập phương có cùng chiều cao nên ta chỉ cần chú ý đến mặt đáy như hình vẽ bên. Đường tròn đáy của hình trụ có bán kính bằng một nửa đường chéo của hình vuông
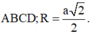 Do đó thể tích hình trụ cần tìm bằng
Do đó thể tích hình trụ cần tìm bằng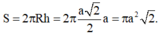
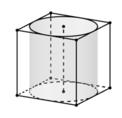





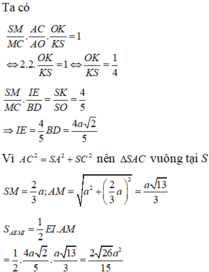
Gọi cạnh của hình vuông có diện tích \(S_k\) là \(a_k\) thì \(a_{k+1}=\dfrac{a_k}{\sqrt{2}}\)
\(\Rightarrow S_{k+1}=\dfrac{1}{2}S_k\)
Do đó:
\(S=S_1+\dfrac{1}{2}S_1+...+\dfrac{1}{2^{19}}S_1\)
\(=a^2\left(1+\dfrac{1}{2}+...+\dfrac{1}{2^{19}}\right)=a^2\left(2-\dfrac{1}{2^{19}}\right)\)