Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A.
Theo quy tắc hình bình hành ta có 
Do đó
(
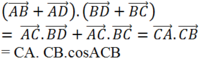
vì AC và BD vuông góc với nhau)
Mặt khác 
và theo định lý Pitago ta có:
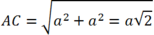
Suy ra 
a, \(AC=\dfrac{AB}{sin45^o}=\dfrac{a}{\dfrac{\sqrt{2}}{2}}=a\sqrt{2}\)
\(\overrightarrow{AB}.\overrightarrow{AC}=AB.AC.cos\widehat{BAC}=a.a\sqrt{2}.cos45^o=a^2\)
b, \(\left(\overrightarrow{AB}+\overrightarrow{AD}\right)\left(\overrightarrow{BD}+\overrightarrow{BC}\right)=\overrightarrow{AC}\left(\overrightarrow{BD}+\overrightarrow{BC}\right)\)
\(=\overrightarrow{AC}.\overrightarrow{BD}+\overrightarrow{AC}.\overrightarrow{BC}\)
\(=AC.BD.cos90^o+AC.AD.cos45^o\)
\(=a\sqrt{2}.a\sqrt{2}.0+a\sqrt{2}.a.\dfrac{\sqrt{2}}{2}=a^2\)
c, \(\overrightarrow{AB}.\overrightarrow{BD}=AB.BD.cos135^o=-a.a\sqrt{2}.\dfrac{\sqrt{2}}{2}=-a^2\)
d, \(\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\left(2\overrightarrow{AD}-\overrightarrow{AB}\right)=\overrightarrow{BC}.\left(\overrightarrow{AD}+\overrightarrow{BD}\right)\)
\(=\overrightarrow{BC}.\overrightarrow{AD}+\overrightarrow{BC}.\overrightarrow{BD}\)
\(=AD^2+BC.BD.cos45^o\)
\(=a^2+a.a\sqrt{2}.\dfrac{\sqrt{2}}{2}=2a^2\)
e, \(\left(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\right)\left(\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}\right)\)
\(=\left(\overrightarrow{AC}+\overrightarrow{AC}\right)\left(\overrightarrow{DB}+\overrightarrow{DB}\right)\)
\(=4.\overrightarrow{AC}.\overrightarrow{DB}=4.AC.DB.cos90^o=0\)
1.
\(\overrightarrow{AB}.\overrightarrow{BC}=\overrightarrow{AB}.\left(\overrightarrow{BA}+\overrightarrow{AC}\right)=\overrightarrow{AB}.\left(-\overrightarrow{AB}\right)+\overrightarrow{AB}.\overrightarrow{AC}=-AB^2=-25\)
2.
\(\overrightarrow{AB}.\overrightarrow{BD}=\overrightarrow{AB}\left(\overrightarrow{BA}+\overrightarrow{AD}\right)=-\overrightarrow{AB}.\overrightarrow{AB}+\overrightarrow{AB}.\overrightarrow{AD}=-AB^2+0=-64\)
Đáp án D
D M → . B C → = D A → + A M → . B C → = D A → . B C → + A M → . B C →
= a . a . c os180 0 + A M . B C . c os 90 0 = − a 2 + 0 = − a 2
a) Ta có:
\(\overrightarrow {DM} = \overrightarrow {DA} + \overrightarrow {AM} = - \overrightarrow {AD} + \frac{1}{2}\overrightarrow {AB} \) (do M là trung điểm của AB)
\(\overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {BN} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {BC} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} \) (do N là trung điểm của BC)
b)
\(\begin{array}{l}\overrightarrow {DM} .\overrightarrow {AN} = \left( { - \overrightarrow {AD} + \frac{1}{2}\overrightarrow {AB} } \right).\left( {\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} } \right)\\ = - \overrightarrow {AD} .\overrightarrow {AB} - \frac{1}{2}{\overrightarrow {AD} ^2} + \frac{1}{2}{\overrightarrow {AB} ^2} + \frac{1}{4}\overrightarrow {AB} .\overrightarrow {AD} \end{array}\)
Mà \(\overrightarrow {AB} .\overrightarrow {AD} = \overrightarrow {AD} .\overrightarrow {AB} = 0\) (do \(AB \bot AD\)), \({\overrightarrow {AB} ^2} = A{B^2} = {a^2};{\overrightarrow {AD} ^2} = A{D^2} = {a^2}\)
\( \Rightarrow \overrightarrow {DM} .\overrightarrow {AN} = - 0 - \frac{1}{2}{a^2} + \frac{1}{2}{a^2} + \frac{1}{4}.0 = 0\)
Vậy \(DM \bot AN\) hay góc giữa hai đường thẳng DM và AN bằng \({90^ \circ }\).
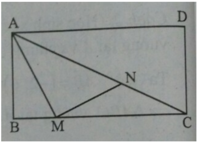
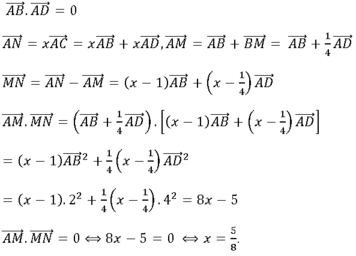
Chọn A.
Chú ý: Nếu có đúng bốn phương án như trong đề thi thì có thể dự đoán ngay phương án A sau khi vẽ hình