Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAED có
\(\widehat{AED}+\widehat{EAD}+\widehat{EDA}=180^0\)
hay \(\widehat{AED}=90^0\)

Bài 2:
a: \(\widehat{ABE}=\widehat{CBE}=\dfrac{\widehat{ABC}}{2}=\dfrac{60^0}{2}=30^0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\widehat{CFE}=60^0\\\widehat{AEB}=\widehat{CEF}=60^0\end{matrix}\right.\)
=>ΔCFE đều
b: Xét tứ giác ABCD có
\(\widehat{BAC}=\widehat{BDC}=90^0\)
Do đó: ABCD là tứ giác nội tiếp

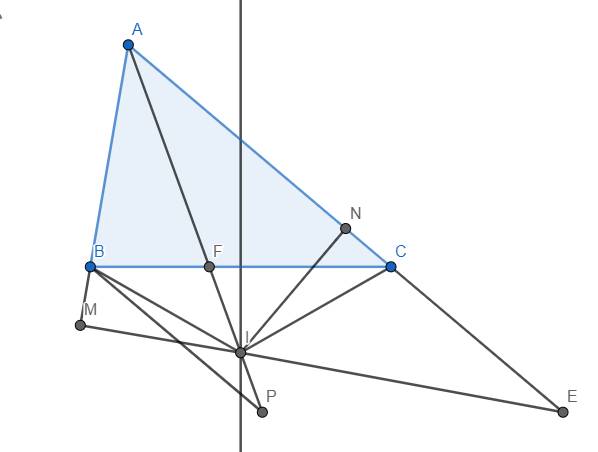
a) Do I nằm trên trung trực của đoạn BC nên \(IB=IC\).
Xét 2 tam giác IAM vuông tại M và IAN vuông tại N, ta có:
AI là cạnh chung và \(\widehat{MAI}=\widehat{NAI}\) (do AI là phân giác góc BAC)
\(\Rightarrow\Delta IAM=\Delta IAN\left(ch-gn\right)\) \(\Rightarrow IM=IN\).
Lại xét 2 tam giác IMB vuông tại M và INC vuông tại N, có:
\(IB=IC\left(cmt\right);IM=IN\left(cmt\right)\)
\(\Rightarrow\Delta IMB=\Delta INC\left(ch-cgv\right)\) \(\Rightarrow MB=NC\left(đpcm\right)\)
b) Ta đã có \(IN\perp AE\) tại N nên ta chỉ cần chứng minh N là trung điểm của đoạn AE là xong. Thật vậy, ta có \(MB=NC\left(cmt\right)\) và \(AB=EC\left(gt\right)\) nên suy ra \(AB+MB=NC+EC\) hay \(AM=NE\).
Mặt khác, do \(\Delta IAM=\Delta IAN\left(cmt\right)\Rightarrow AM=AN\)
Từ đó suy ra \(AN=NE\) hay N là trung điểm AE. Ta có đpcm.
c) Qua B kẻ đường thẳng song song với AC cắt AI tại P. Khi đó ta có \(\widehat{BAP}=\widehat{CAP}=\widehat{BPA}\) nên tam giác ABP cân tại B, suy ra \(AB=BP\). Mặt khác, theo định lý Thales, ta có \(\dfrac{FB}{FC}=\dfrac{BP}{AC}=\dfrac{AB}{AC}< 1\) (do \(AB< AC\)) nên suy ra \(\dfrac{FB}{FC}< 1\) hay \(FB< FC\) (đpcm)

a: Xét ΔBAC có BM là phân giác
nên \(\dfrac{AM}{AB}=\dfrac{CM}{CB}\)
=>\(\dfrac{AM}{5}=\dfrac{CM}{2}\)
mà AM+CM=AC=5
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AM}{5}=\dfrac{CM}{2}=\dfrac{AM+CM}{5+2}=\dfrac{5}{7}\)
=>\(AM=5\cdot\dfrac{5}{7}=\dfrac{25}{7}\left(cm\right);CM=2\cdot\dfrac{5}{7}=\dfrac{10}{7}\left(cm\right)\)
b: Ta có: \(\widehat{ABM}=\widehat{MBC}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{ACN}=\widehat{NCB}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABM}=\widehat{MBC}=\widehat{ACN}=\widehat{NCB}\)
Xét ΔABM và ΔACN có
\(\widehat{ABM}=\widehat{ACN}\)
AB=AC
\(\widehat{BAM}\) chung
Do đó: ΔABM=ΔACN
=>AM=AN
Xét ΔABC có \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
nên MN//BC
tớ ko biết