E
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 2 2022
Xét ΔANF có ME//NF
nên ME/NF=AM/AN
=>5/NF=1/2
=>NF=10(cm)
Xét ΔANF có
M là trung điểm của AB
ME//NF
Do đó: E là trung điểm của AF
Xét hình tahng BMEC có
N là trung điểm của MB
NF//ME//BC
Do đó: F là trung điểm của EC
Xét hình thang BMEC có
N là trung điểm của MB
F là trung điểm của EC
Do đó: NF là đường trung bình
=>ME+BC=2NF
=>BC=2NF-ME=20-5=15(cm)
CT
27 tháng 10 2018
Bạn dựa vào dtb của tam giác nha
Ta có ME//BC ; NF//BC
=>ME//NF
Xét tam giác ANF có
AM = MN
ME//NF (cmt)
=> AE = EF
Ta có tam giác ANF
AM = MN (gt)
AE = EF (cmt)
=> ME là dtb của tam giác ANF
=> ME = \(\dfrac{NF}{2}=\dfrac{5}{2}=2,5\left(cm\right)\)
@Akai Haruma
27 tháng 3 2020
Kẻ MP//MD (P \(\in\)AD) ta có:
\(\frac{AM}{AB}=\frac{AP}{AD}\)mà \(\frac{AM}{AB}=\frac{CN}{CD}\left(gt\right)\)nên \(\frac{AP}{AD}=\frac{CN}{CD}\)=> NP//AC
Gọi giao của MP và AC là K, của NP và BD là H
\(\frac{MK}{PK}=\frac{OB}{OD}\)và \(\frac{NH}{HP}=\frac{OC}{OA}\)mà \(\frac{OB}{OD}=\frac{OC}{OA}\)
=> \(\frac{MK}{KP}=\frac{NH}{HP}\)do đó KH//MN
Các tứ giác MKHF và EKHN là hình bình hành nên
MF=HK và EN=KH => MF=EN
Do đó: ME=NF (đpcm)
CM
17 tháng 3 2017
Ta có: MN // BC (gt), áp dụng hệ quả của định lý Ta – lét suy ra:
Suy ra: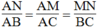 
(Hệ quả định lí Ta-lét)
